ЛЕКЦИЯ 12. Затухающие и вынужденные колебания

Затухающие и вынужденные колебания. Резонанс.

В любой колебательной системе со временем происходит затухание колебаний, обусловлен-ное потерей энергии под действием неконсервативных сил. Рассмотрим затухание колеба-ний материальной точки под действием силы вязкого трения (лекция 10)

.

В этом случае 2-ой закон Ньютона для материальной точки под действием возвращающей сил и силы трения в проекции на ось 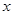можно представить в виде

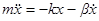. (1)

Коэффициент 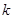необязательно должен иметь смысл коэффициента жесткости. Он может описывать возвращающую силу любой природы.

Можно показать, что при условии 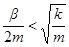решение уравнения (1) имеет вид

,

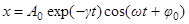где 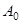- начальная амплитуда колебаний, 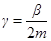- коэффициент затухания, 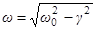- частота затухающих колебаний, 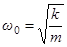- собственная частота.

Функция 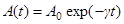представляет собой амплитуду затухающих колебаний (рис. 1). Для характеристики скорости затухания колебаний вводится логарифмический декремент затухания

.

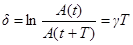Затухающие колебания существуют при выполнении условия 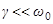. При 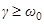имеет место апериодический процесс, при котором точка возвращается в положение равновесия, не совершив ни одного колебания.

Дата добавления: 2013-12-13