Первое начало термодинамики. теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил

Первое начало термодинамики

Первое начало термодинамики - это закон сохранения и превращения энергии в термодинамических процессах.

Изменить внутреннюю энергию системы можно двумя способами: совершая над системой работу (например, сжимая газ в цилиндре, с помощью поршня) или сообщая системе теплоту (например, нагревая газ в герметичном сосуде).

Рассмотрим замкнутую макроскопически неподвижную систему не находящуюся во внешних силовых полях и проанализируем с энергетической точки зрения равновесный процесс перехода системы из какого-либо начального состояния 1в другое состояние 2.

Изменение внутренней энергии системы ∆ U=U₂-U₁ в таком процессе равно разности между количеством теплоты Q, полученным системой, и работой А, совершенной системой против внешних сил

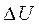=Q-A или Q= 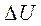+ A

В дифференциальной форме: ,

где dU (полный дифференциал) -бесконечно малое изменение внутренней энергии системы, δA- элементарная работа, δQ- бесконечно малое количество теплоты. δА и δ Qне являются полными дифференциалами.

Дело в том, что внутренняя энергия системы является однозначной функцией состояния системы. Отсюда следует, что при совершении системой произвольного процесса, в результате которого она вновь возвращается в исходное состояние, полное изменение внутренней энергии системы равно нулю 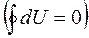. Ни работа, ни теплота не являются функциями состояния системы.

Все величины входящие в первое начало термодинамики могут быть как положительными, так и отрицательными.

Если к системе подводится теплота, то δQ >0; если от системы отводится теплота, то δQ < 0.

Если система совершает работу над внешними телами, то δА > 0, если же над системой внешние силы совершают работу, то δА < 0.

Другая формулировка пер вого начала термодинамики связана с тем, что если система периодически возвращается в первоначальное состояние, и следовательно 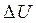=0, то А =Q, т.е. вечный двигатель первого рода - периодически действующий двигатель, который совершал бы большую работу, чем сообщенная ему извне энергия, - невозможен.

5. Работа газа при его расширении.

Если находящийся под поршнем в цилиндрическом сосуде, газ, расширяясь, 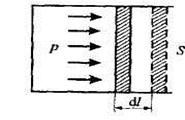передвигает поршень на расстояние dl, то производит над ним работу δ А = Fdl=pSdl = pdV, где S - площадь поршня.

Полная работа А, совершаемая газом при изменении его объема от V₁до V₂:

Равновесные процессы – это процессы, состоящие из последовательности равновесных состояний. Они протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессы неравновесны, но в ряде случаев (достаточно медленные процессы) неравновесностью реальных процессов можно пренебречь.

Равновесные процессы можно изображать графически в координатах (p,V). Так работа δ A=pdV определяется площадью заштрихованной полоски, а полная работа - площадью под кривой между V₁и V₂.

При неравновесных п роцессах значения параметров в разных частях системы различны и не существует (р,К)-точек, характеризующих состояние всей системы. Поэтому графическое изображение неравновесного процесса невозможно.

6. Теплоемкость.

Удельная теплоемкость вещества с - величина, равная количеству теплоты, необходимому для нагревания 1кг вещества на 1 К. Единица удельной теплоемкости - Дж/(кг ·К)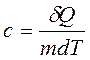

Молярная теплоемкость С_μ - величина, равная количеству теплоты, необходимому для нагревания 1моль вещества на 1 К. Единица молярной теплоемкости - Дж/(моль К).

Связь между С_μ и с : С _μ = сμ

Различают теплоемкости (удельную и молярную) при постоянном объеме (с_v и С_V) и при постоянном давлении (с_p и С_p), если в процессе нагревания вещества его объем или давление поддерживаются постоянными.

30. Молярная теплоемкость при постоянном объеме.

Из первого начала термодинамики δQ =dU+δA, с учетом δ A = pdV и , для 1 моль газа получим: .

При V = const работа внешних сил δAравна нулю и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии.

С_V равна изменению внутренней энергии 1моль газа при повышении его температуры на 1К.

Поскольку dU_μ = i/2RdT, то

31. Молярная теплоемкость при постоянном давлении. Уравнение Майера.

Если газ нагревается при р = const, то

не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от р, ни от V, а определяется только Т) и всегда равна С_V. Дифференцируя уравнение Клапейрона - Менделеева рV_μ=RT по Т при р=const, получим

С_P =C_V+R - уравнение Майера

С_P всегда больше C_V - на величину универсальной газовой постоянной.

Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа.

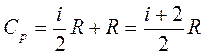
При рассмотрении термодинамических процессов важную роль играет величина

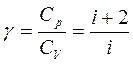
которая называется коэффициентом Пуассона.

ИЗОПРОЦЕССЫ Рассмотрим равновесные процессы, происходящие с термодинамическими системами, при которых один изосновных параметров состояния сохраняется постоянным.

32- Изохорный процесс (V = const).

Диаграмма этого процесса - изохора - в коор­динатах (p,V) изображается прямой, параллельной оси ординат (ось р). Процесс 2-1 - изохорный нагрев, процесс 2-3 — изохорное охлаждение.

При изохорном процессе газ не совершает работу над внешними телами (δA=pdV=0) и вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии (δQ=dU). Поскольку dU_μ =C_VdT, то для произвольной массы газа:

33. Изобарный процесс (р = const).

Диаграмма этого процесса - изобара - в координатах (р,V) изобра­жается прямой параллельной оси абсцисс (ось V). При изобарном процессе работа газа при увеличении объема от V₁ до V₂ равна:

и определяется площадью заштрихованного прямоугольника. Используя уравнение Клапейрона pV=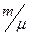RT, получаем V ₂ – V₁= 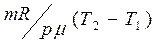, отсюда

Физический смысл универсальной газовой постоянной: R численно равна работе изобарного расширения 1моля идеального газа при нагревании его на 1 К.

34. Изотермический процесс (Т = const).продолжить

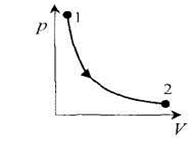
диаграмма этого процесса - изотерма - в коор­динатах (p,V) представляет собой гиперболу. Изотермический процесс описывается законом Бойля-Мариотта (pV= const).

Работа изотермического расширения газа

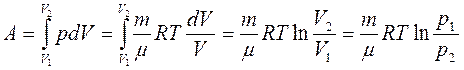
Так как при T=const внутренняя энергия идеального газа не изменяется, то из первого начала термодинамики следует, что δ Q=δA, to есть все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил.

Поэтому, для того, чтобы при расширении газа температура не понижалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.

35. Адиабатический процесс (δQ=0).

Адиабатическим называется процесс, при котором отсутствует теплообмен между системой и окружающей средой (δQ = 0).

К адиабатическим процессам можно отнести все быстропротекающие процессы (теплообмен не успевает совершиться), например, распространение звука в среде, циклы расширения и сжатия в двигателях внутреннего сгорания, в холодильных установках и т. д.

Из первого начала термодинамики следует, что при адиабатическом процессе δ A = -dU. Используя δ А = pdV и dU =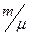C_vdT, получим

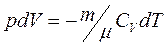(1). С другой стороны, из 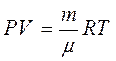следует (2). Разделив (2) на (1) получим:

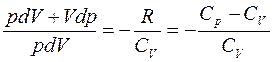или , где - коэффициент Пуассона. Интегрирование этого уравнения дает , откуда следует уравнение Пуассона уравнение адиабатического процесса. =const

Используя уравнение Менделеева- Клапейрона pV = RT, получаем: =const

Диаграмма адиабатического процесса - адиабата - в координатах (р,V) изображается гиперболой. Адиабата (р=const) более крута, чем изотерма (рV=const). Это объясняется тем, что при адиабатическом сжатии 1-3 увеличение давления газа обусловлено не только уменьшением его объема, но и повышением температуры.

36. Работа газа в адиабатическом процессе.

В адиабатическом процессе δ A=-dU, поэтому . Если газ адиабатически расширяется от объема V₁, до V ₂, то его температура уменьшается от T₁, до T₂, и работа расширения идеального газа

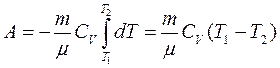
Откуда получаем, используя уравнение Менделеева –Клапейрона pV = RT.

Работа адиабатического расширения 1-2 (заштрихованная площадь) меньше, чем при изотермическом процессе. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом расширении температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

37. Политропические процессы (С = const).

Процесс, в котором теплоемкость остается постоянной (С= const) называется политропическим.

Рассмотренные выше изохорный, изотермический, изобарный и адиабатический процессы - это частные случаи политропного процесса.

Дата добавления: 2013-12-13