Круговой процесс (цикл)

Уравнение политропы

pVⁿ = const

где коэффициент п = 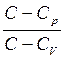называется показателем политропы.

Значения теплоемкости и показателя политропы для разных процессов приведены в таблице.

Теплоемкость при изотермическом процессе бесконечно велика, поскольку dT=0, в то время как .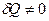

Теплоемкость при адиабатическом процессе равна нулю, поскольку 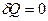, в то время как

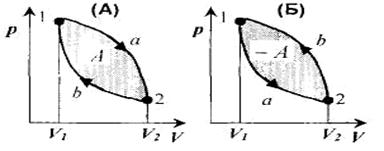
Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное состояние. На (p,V) -диаграмме цикл изобража­ется замкнутой кривой, где участок 1-2 соответствует расширению, а 2-1 - сжатию газа.

Работа расширения А₁ положительна: A₁ >0.

Работа сжатия отрицательна: А₂ <0.

Работа за цикл А определяется площадью, охватываемой замкнутой кривой:

А = А₁+А₂

Таким образом, работа -это функция не только состояния термодинамической системы, но и вида процесса, который происходит. Поэтому работа не является однозначной функцией состояния (такой, как внутренняя энергия). Из первого начала термодинамики следует, что теплота Q, так же как и работа А, является функцией процесса, который происходит с системой.

Цикл называется прямым, если за цикл совершается положительная работа А = pdV > 0 (цикл протекает по часовой стрелке - рисунок (А)).

Цикл называется обратным, если за цикл совершается отрицательная работа А = pdV < 0 (цикл протекает против часовой стрелки - рисунок (Б)).

Прямой цикл используется в тепловых двигателях (совершают работу за счет полученной извне теплоты). Обратный цикл используется в холодильных машинах (за счет работы внешних сил теплота переносится к телу с более высокой температурой).

39. КПД кругового процесса.

В результате кругового процесса система возвращается в исходное состояние, следовательно, полное изменение внутренней энергии равно нулю. Поэтому Q=∆U+А=А, т.е. работа, совершаемая за цикл, равна количеству полученной извне теплоты. Если в ходе кругового процесса система не только получает количество теплоты Q₁, но и теряет (отдает) количество теплоты Q ₂,

то Q=Q₁-Q₂.

Термический коэффициент полезного действия для кругового процесса - это величина, равная отношению работы, совершенной системой, к количеству теплоты, полученному в этом цикле системой:

40. Обратимый и необратимый процессы.

Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении. Причем, если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.

Реальные процессы необратимы, в них всегда происходит диссипация (потеря) энергии (из-за трения, теплопроводности и т.д.). Обратимые процессы - это физическая модель - это идеализация реальных процессов.

41. Энтропия.

Количество тепла δQ, которое должно быть доставлено системе или отнято у неё при переходе от одного состояния в другое, не определяется однозначно начальным и конечным состояниями, но существенно зависит от способа осуществления этого перехода (δQне является функцией состояния системы).

Однако, приведенное количество теплоты - отношение теплоты δQ к температуре Т системы при бесконечно малых изменениях состояния системы - есть функция состояния системы. В любом обратимом круговом процессе

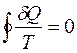
Следовательно, подынтегральное выражение есть полный дифференциал некоторой функции, которая определяется только начальным и конечным состояниями системы и не зависит от пути, каким система пришла в это состояние.

Энтропией S называется функция состояния системы, дифференциалом которой является δQ/T:

Т.о. первое начало термодинамики δ Q = dU + δА можно записать в виде

TdS = dU + δA,

откуда

Функция F=U-TS является функцией состояния системы и называется энергией Гельмгольца или свободной энергией.

42. Изменение энтропии.

В замкнутой системе для обратимых процессов ; для необратимых циклов ∆S >0.

Неравенство Клаузиуса: энтропия замкнутой системы может либо возрастать (в случае необратимых процессов) либо оставаться постоянной (в случае обратимых процессов).

Поскольку dS и δQимеют один и тот же знак, то по характеру изменения энтропии можно судить о направлении процесса теплообмена. При нагревании тела δQ>0и его энтропия возрастает dS>0, при охлаждении δ Q<0 и энтропия тела убывает dS < 0.

Изоэнтропийным называется процесс, протекающий при постоянной энтропии (S = const).

В обратимом адиабатическом процессе δQ= ТdS=0, так что dS=0 и S = const, поэтому адиабатический процесс является изоэнтропийным.

Рассмотрим для примера идеальный газ, который совершает равновесный переход из состояния 1 в состояние 2. Изменение его энтропии

используя dU =; ; 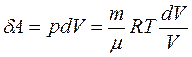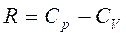и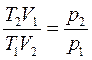

43. Статистическое толкование энтропии.

Термодинамическая вероятность W состояния тела или системы -это число способов, которыми может быть реализовано данное конкретное термодинамическое состояние (макросостояние). Иначе говоря, это число всевозможных микрораспределений частиц по координатам и скоростям (микросостояний), которыми может быть осуществлено данное макросостояние.

Формула Больцмана: S = k ln W

где k - постоянная Больцмана.

Энтропия системы определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние.

Энтропия является мерой неупорядоченности системы, -чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия.

44. Принцип возрастания энтропии.

Все процессы в замкнутой системе ведут к увеличению её энтропии. В замкнутой системе идут в направлении от менее вероятных состояний к более вероятным, до тех пор, пока вероятность состояния не станет максимальной. В состоянии равновесия — наиболее вероятного состояния системы - число микросостояний максимально, при этом максимальна и энтропия.

45. Второе начало термодинамики.

Любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает (закон возрастания энтропии).

Первое начало термодинамики выражает закон сохранения и превращения энергии применительно к термодинамическим процессам.

Второе начало термодинамики определяет направление протекания термодинамических процессов, указывая, какие процессы в природе возможны, а какие - нет.

Существуют ещё две формулировки второго начала термодинамики, эквивалентных закону возрастания энтропии:

1) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной
от нагревателя, в эквивалентную ей работу;

2) по Клаузиусу: невозможен круговой процесс, единственным
результатом которого является передача теплоты от менее
нагретого тела к телу более нагретому.

46. Третье начало термодинамики.

Третье начало термодинамики - теорема Нернста-Планка -постулирует поведение термодинамических систем при нуле Кельвина (абсолютном нуле): энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина.

Теплоемкости С_V и С_p при Т = 0 К равны нулю, поскольку:

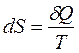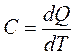, , , S(V=const, T) =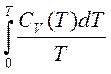

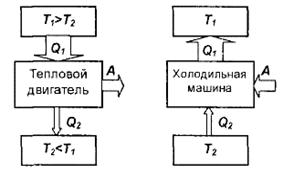
47. Тепловые двигатели и холодильные машины.

Тепловой двигатель — это периодически действующий двигатель, совершающий работу за счет полученной извне теплоты.

Термостатом называется термодинамическая система, которая может обмениваться теплотой с телами практически без изменения собственной температуры.

Рабочее тело — это тело, совершающее круговой процесс и обменивающееся энергией с другими телами.

Принцип работы теплового двигателя: от термостата с более высокой температурой Т₁, называемого нагревателем, за цикл отнимается количество

теплоты Q₁, а термостату с более низкой температурой Т₂, называемому холодильником, за цикл передается количество теплоты Q₂, при этом

совершается работа A = Q₁ –Q₂,.

Термический КПД двигателя:

Чтобы КПД был равен 1, необходимо, чтобы Q₂=0, а это запрещено вторым началом термодинамики.

Процесс, обратный происходящему в тепловом двигателе, используется в холодильной машине: от термостата с более низкой температурой Т₂, за цикл отнимается количество теплоты Q₂ и отдается термостату с более высокой температурой Т₁, > Т₂,. При этом Q = Q₁ - Q₂ = А или Q₁ = Q₂ + A

Количество теплоты Q₁, отданное системой термостату T_t, больше количества теплоты Q₂, полученного от термостата Т_г на величину работы, совершенной над системой.

Эффективность холодильной машины характеризует холодильный коэффициент η' - отношение отнятой от термостата с более низкой температурой количества теплоты Q₂ к работе А, которая затрачивается на приведение холодильной машины в действие:

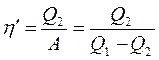
48. Теорема Карно

Из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей Т, и холодильников Т₂, наибольшим КПД обладают обратимые машины. При этом КПД обратимых машин, работающих при одинаковых температурах нагревателей и холодильников, равны друг другу и не зависят от природы рабочего тела, а определяются только температурами нагревателя и холодильника.

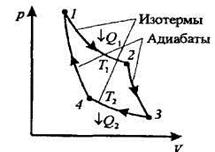
Наиболее экономичный обратимый круговой процесс, состоящий из двух изотерм и двух адиабат.

Рассмотрим прямой цикл Карно, в котором в качестве рабочего тела используется идеальный газ, заключенный в сосуд с подвижным поршнем.

Последовательные термодинамические процессы в цикле Карно

1-изотерма-2-адиабата-3-изотерма-4-адиабата-1:

А = А₁₂+ A₂₃+A₃₄ + A₄₁ =Q₁+A₂₃ - Q₂+ A₂₃ = Q₁ – Q₂

Для адиабат 2-3 и 4-1 уравнения Пуассона: , , 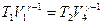откуда

V₁/ V₂ = V₃/V₄.

Используя это, термический КПД цикла Карно:

действительно определяется только температурами нагревателя и холодильника.

Дата добавления: 2013-12-13