Шестиугольник Паскаля

Определение типа коники

Коники – кривые 2-ого порядка. Типы коник: эллипс (окружность), гипербола, парабола. Кониками их называют, поскольку все они являются сечениями конуса (материал предыдущих лекций). Метриками коники называют оси, точки фокусов, директрисы.

Все коники являются плоскими кривыми.

Получив конику в пересечении нужно уметь определить ее тип и метрики. AutoCAD умеет определять эллипс и окружность при пересечении штатных квадрик: конус, сфера, цилиндр. Во всех остальных случаях коники формируются как сплайны, без опознавания их типа. В том числе и эллипсы для нештатных квадрик: параболоидов, гиперболоижов, эллипсоидов. В этих случаях можно определить тип коники в следующей последовательности:

1. проверить, что кривая плоская: установить ПСК по трем точкам кривой с привязкой Ближайшая. Командой Лист измерить координаты точек;.
2. по шестиугольнику Паскаля убедиться, что кривая является коникой;
3. методом хорд определить тип коники.

Теорема Паскаля (1623–1662) – одна из основных теорем проективной геометрии – науки, рассматривающей общие закономерности проецирования объектов. Б. Паскалю не было еще 17 лет, когда он сформулировал эту теорему, отражающую общие свойства коник [см. интернет, Блез Паскаль – французский философ, писатель, математик и физик. В его честь в наше время назван известный язык программирования].

Теорема заключается в том, что построив произвольный шестиугольник по точкам коники и соединив определенным образом его стороны, получим совпадение диагоналей шестиугольника в прямую линию.

Рассмотрим действие теоремы на примере имеющейся в AutoCAD’е коники – эллипса (можно взять окружность), для которого AutoCAD гарантирует предельную точность построения 10^-8.

Привести пример построения шестиугольника Паскаля для штатного эллипса, вариант а) и б). Построения выполняем на листе в том же файле, где получены сечения гиперболоида.

1. Построим произвольный эллипс (ellipse). Нанесите на нем (привязка Nearest) маркеры шести точек. Проставьте рядом с маркерами номера точек в произвольной последовательности, то есть не обязательно в порядке их расположения. На рис. 1.9 показано как одни и те же точки на эллипсе пронумерованы различно. Вы можете расположить и пронумеровать точки иначе. Важно только, чтобы каждая точка принадлежала проверяемой линии. Для этого маркеры точки должны быть заданы с объектной привязкой Nearect.
2. Командой line соединяем точки отрезками прямых по порядку принятой нумерации, то есть в последовательности 1-2-3-4-5-6-1. Последний отрезок 6-1 замыкает ломаную линию, образуя шестиугольник Паскаля. Для каждого варианта нумерации образуется свой шестиугольник. Концы отрезков указываем с объектной привязкой Node по проставленным маркерам точек.
3. Находим три точки пересечения следующих пар отрезков: А=(1-2)∩(4-5); B= (2-3) ∩ (5-6); C=(3-4) ∩(6-1). Указанные точки могут находиться как на пересечении отрезков, так и на их продолжении.

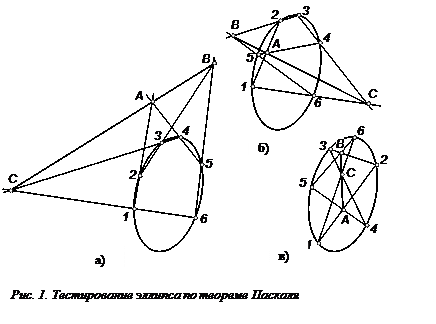Согласно теореме Паскаля, если линия является коникой, то точки A,B,C располагаются на одной прямой. Проверяем. Соединяем точки A,B,C отрезками прямых (line), указывая каждую точку с привязкой Intersection. Последовательность соединения точек такова, чтобы отрезки расположились последовательно, без перекрытия. Это C-A-B для примера на рис 1.9, а,б и A-C-B для рис. 1.9, в. Командой units задаем предельную точность измерения углов, равную 10^-8. Командой list определяем свойства отрезков построенных отрезков, соединяющих точки A,B,C. Находим в выводимой информации для каждого отрезка угол с осью Х, измеренный в плоскости XY (Angle in XY Plane). Убеждаемся, что в рассмотренном примере для штатного эллипса эти углы равны между собой с предельной точностью, то есть проверяемые отрезки принадлежат одной прямой (прямой Паскаля).

Привести пример шестиугольника Паскаля для сплайна-эллипса как сечения гиперболоида.

1. Показать, что это плоская кривая.
2. Построив для нее шестиугольник Паскаля, показать, что это коника. Отметить, что погрешность построения коник как сплайнов, измеряемая по углу, в AutoCAD'е составляет 10^-3...10^-5.

Дата добавления: 2013-12-14