
- Р Р‡.МессенРТвЂВВВВВВВВжер
- ВКонтакте
- РћРТвЂВВВВВВВВнокласснРСвЂВВВВВВВВРєРСвЂВВВВВВВВ
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВВВРЎР‚
- LiveJournal
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частные производные высших порядков
|
|
|
|
Частные производные функции в свою очередь являются функциями, и поэтому можно рассматривать их частные производные. Например, у функции 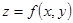 могут существовать частные производные
могут существовать частные производные 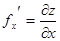 ,
, 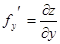

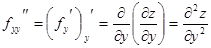
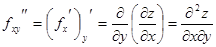
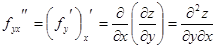 .
.
Производные  называются частными производными второго порядка. Аналогично определяются производные более высоких порядков.
называются частными производными второго порядка. Аналогично определяются производные более высоких порядков.
Оказывается, что при достаточно общих условиях результат дифференцирования по различным переменным не зависит от выбора порядка переменных, по которым происходит дифференцирование.
| Теорема | Если функция 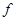 определена вместе со своими частными производными определена вместе со своими частными производными  , , 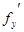 , , 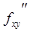 и и  в некоторой окрестности точки в некоторой окрестности точки 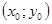 и производные и производные 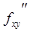 и и  непрерывны в этой точке, то непрерывны в этой точке, то
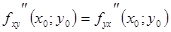 . .
|
Из этой теоремы в случае непрерывности соответствующих частных производных следует независимость результата дифференцирования от порядка переменных, по которым проводится дифференцирование, для функции любого числа переменных и для частных производных любого порядка.
Пример. 

Решение:
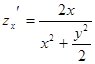 ,
, 
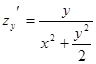 ,
, 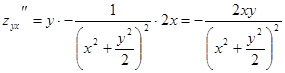 .
.
|
|
|
Дата добавления: 2014-01-04; Просмотров: 297; Нарушение авторских прав?; Мы поможем в написании вашей работы!