
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Достаточные условия экстремума функции
|
|
|
|
| Опр. | Квадратичная форма 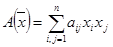 , , 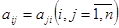 называется положительно (отрицательно) определенной, если для называется положительно (отрицательно) определенной, если для  выполняется неравенство выполняется неравенство  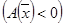 . .
|
Положительно и отрицательно определенные квадратичные формы называются знакоопределенными.
| Опр. | Квадратичные формы, принимающие как положительные, так и отрицательные значения, называются знакопеременными. |
| Теорема | Пусть функция 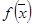 дважды непрерывно дифференцируема в окрестности критической т. дважды непрерывно дифференцируема в окрестности критической т. 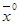 . Тогда, если второй дифференциал . Тогда, если второй дифференциал
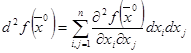 функции
функции 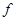 является положительно (отрицательно) определенной квадратичной формой, то является положительно (отрицательно) определенной квадратичной формой, то 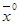 есть точка строгого есть точка строгого  . Если второй дифференциал . Если второй дифференциал  - знакопеременная квадратичная форма, то в т. - знакопеременная квадратичная форма, то в т. 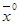 экстремума нет. экстремума нет.
|
Рассмотрим случай функции двух переменных  и сформулируем для него достаточные условия в терминах, удобных для применения.
и сформулируем для него достаточные условия в терминах, удобных для применения.
| Теорема | Пусть в некоторой область, содержащей т. 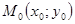 функция функция  имеет непрерывные частные производные до третьего порядка включительно; пусть, кроме того, т. имеет непрерывные частные производные до третьего порядка включительно; пусть, кроме того, т. 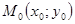 - критическая точка - критическая точка  (т.е. (т.е. 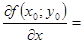 = = 0) и 0) и 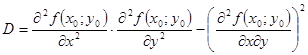 (дискриминант). Тогда:
1) (дискриминант). Тогда:
1)  имеет имеет 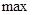 , если: , если:
 и и 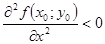 2)
2)  имеет имеет 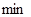 , если: , если:
 и и  3)
3)  не имеет ни не имеет ни 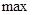 , ни , ни 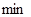 , если: , если:
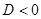 4) если
4) если 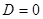 , то экстремума может и не быть (в этом случае проводят специальное исследование). , то экстремума может и не быть (в этом случае проводят специальное исследование).
|
Доказательство:
Положим 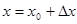 ,
, 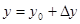 и напишем формулу Тейлора второго порядка для функции
и напишем формулу Тейлора второго порядка для функции  .
.
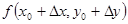 =
= +
+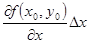 +
+ +
+
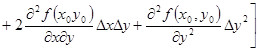 +
+
где 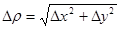 , а
, а  при
при 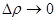 .
.
По условию 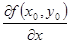 =
= =0
=0 
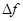 =
=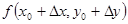 -
- =
= 
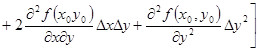 +
+ (1)
(1)
Обозначим: 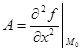 ,
,  ,
, 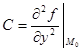 ,
,
Через  - угол между направлением
- угол между направлением 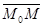
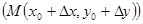 и осью
и осью  , тогда
, тогда  ,
, 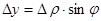 .
.
Подставим эти выражения в формулу для 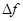 (1):
(1):
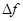 =
=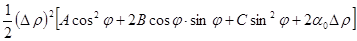 (2)
(2)
Разделив и умножив на  выражение, стоящее в квадратных скобках, получим:
выражение, стоящее в квадратных скобках, получим:
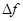 =
=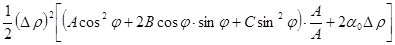 =
=
=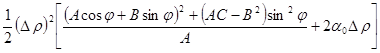 (3)
(3)
Рассмотрим теперь 4 возможных случая:
1) Пусть 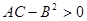 ,
, 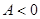 .
.
Тогда в числителе дроби стоит неотрицательная величина. Она в  не обращается т.к. первое слагаемое обращается в 0 при
не обращается т.к. первое слагаемое обращается в 0 при  , а второе при
, а второе при  .
.
Если 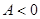 , то дробь есть отрицательная величина, не обращающая в 0. Обозначим её через -
, то дробь есть отрицательная величина, не обращающая в 0. Обозначим её через - 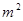 тогда:
тогда:
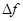 =
= ,
,
где 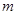 не зависит от
не зависит от  , а
, а  при
при 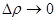 . Следовательно при достаточно малых
. Следовательно при достаточно малых  будет:
будет:
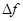
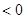
или 
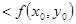 ,
,
т.е. в т. 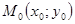
 достигает
достигает 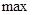 .
.
2) Пусть 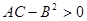 ,
, 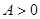 .
.
Тогда аналогично рассуждая, получим:
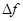 =
=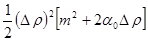
или

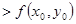
т.е. в т. 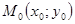
 достигает
достигает 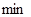 .
.
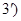 Пусть
Пусть  ,
, 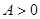 .
.
В этом случае функция возрастает, когда мы движемся из т. 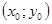 по одним направлениям, и убывает, когда мы движемся по другим направлениям. Действительно, при перемещении вдоль луча
по одним направлениям, и убывает, когда мы движемся по другим направлениям. Действительно, при перемещении вдоль луча  имеем:
имеем:
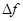 =
=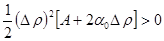
(т.е. функция возрастает)
Если же перемещается вдоль луча  , такого, что
, такого, что 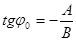 , то при
, то при 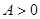 будет:
будет:
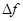 =
=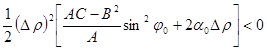
(т.е. функция убывает)
В этом случае нет ни 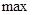 , ни
, ни 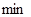 .
.
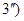 Пусть
Пусть  ,
, 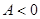 .
.
Исследование проводится так же, как и в случае 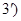 . Функция не имеет ни
. Функция не имеет ни 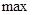 , ни
, ни 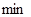 .
.
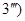 Пусть
Пусть  ,
, 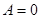 . Тогда
. Тогда 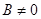 и равенство (2) можно переписать в виде
и равенство (2) можно переписать в виде
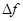 =
= .
.
При достаточно малых значениях  выражение, стоящее в круглых скобках, сохраняет знак, т.к. оно близко к
выражение, стоящее в круглых скобках, сохраняет знак, т.к. оно близко к  , а множитель
, а множитель  меняет знак в зависимости от того, будет ли
меняет знак в зависимости от того, будет ли  больше 0 или меньше 0. следовательно, и в этом случае
больше 0 или меньше 0. следовательно, и в этом случае 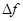 меняет знак при различных
меняет знак при различных  , т.е.
, т.е.  не имеет ни
не имеет ни 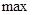 , ни
, ни 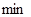 .
.
Если  в т.
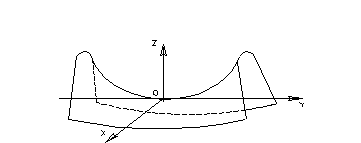
в т. 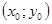 , то в этом случае поверхность, служащая графиком функции, может вблизи этой точки иметь, например, форму седла. Говорят, что функция в этой точке имеет мини-махе.
, то в этом случае поверхность, служащая графиком функции, может вблизи этой точки иметь, например, форму седла. Говорят, что функция в этой точке имеет мини-махе.
4) 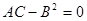 . В этом случае на основании формул (2) и (3) сделать заключение о знаке
. В этом случае на основании формул (2) и (3) сделать заключение о знаке 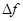 нельзя. Так, например, при
нельзя. Так, например, при  будем иметь:
будем иметь:
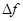 =
= ,
,
при 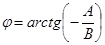 знак
знак 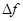 определяется знаком
определяется знаком 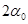 , здесь требуется специальное дальнейшее исследование (например, с помощью формулы Тейлора более высокого порядка или каким – либо иным способом).
, здесь требуется специальное дальнейшее исследование (например, с помощью формулы Тейлора более высокого порядка или каким – либо иным способом).
Пример. 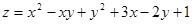 ,
, 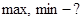
Решение:
1)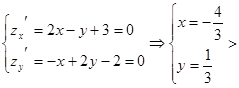 стационарной точки
стационарной точки
2)
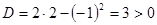 Есть экстремум.
Есть экстремум.
Т.к. 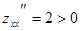 , то это
, то это 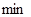
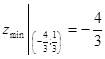 .
.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 332; Нарушение авторских прав?; Мы поможем в написании вашей работы!