Свойства криволинейных интегралов

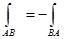
Криволинейный интеграл определяется интегральным выражением, формой кривой интегрирования и указанием направления интегрирования.

При изменении направления интегрирования криволинейный интеграл 2 рода (по координатам) изменяет свой знак, так как при этом вектор 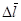, а следовательно, и его проекци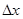и и 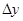меняют знаки.

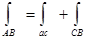
Кривую интегрирования можно разбить на части.

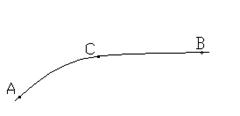
Разобьем кривую 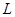точкой С на част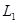и и 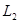так, что 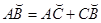. Тогда из формулы (1) следует:

.

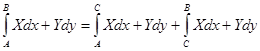Это соотношение справедливо для любого числа слагаемых.

Криволинейный интеграл по замкнутой плоской линии 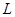при положительном направлении её обихода (против хода часовой стрелки) обозначается ,

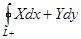а по ходу часовой стрелки .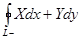

Обыкновенный (прямолинейный) определенный интеграл является частным случаем криволинейного интеграла, у которого линией интегрирования служит прямолинейный отрезок оси координат.

Криволинейный интеграл 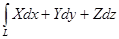можно рассматривать как интеграл от векторной функции 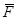, заданной проекциям 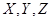, и обозначать символом: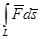

В частности, когда криволинейный интеграл от векторной функции 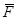берется по замкнутой кривой 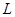, этот криволинейный интеграл называется также циркуляцией вектора 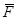по замкнутому контуру .

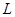Дата добавления: 2014-01-04