
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вычисление криволинейного интеграла
Укажем способ вычисления криволинейного интеграла.
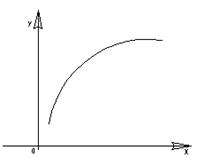
Пусть 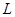 задана в пар-ой форме
задана в пар-ой форме
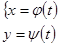 и
и 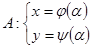
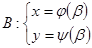
Разделим 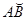 на части
на части 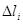 точками
точками 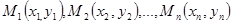 , при этом
, при этом  .
.
Рассмотрим интеграл 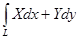 .
.
| Теорема о существовании криволинейного интеграла | Если функция 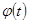 и и 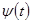 непрерывны и имеют непрерывные производные непрерывны и имеют непрерывные производные 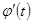 и и 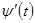 , а также непрерывны функции , а также непрерывны функции  и и 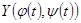 как функции как функции 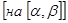 , то существуют пределы , то существуют пределы
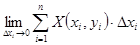 = =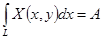 , , 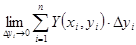 = =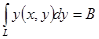 где
где 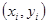 - координаты некоторой точки, лежащей на дуге - координаты некоторой точки, лежащей на дуге 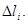 Эти пределы не зависят от способа деления дуги Эти пределы не зависят от способа деления дуги 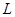 на частные дуги на частные дуги 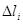 при условии, что при условии, что 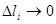 ; не зависит от выбора точки ; не зависит от выбора точки 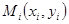 на дуге на дуге 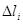 . .
|
(Без доказательств)
Эта теорема дает возможность получить способ для вычисления криволинейного интеграла.
Итак, по определению 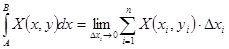 (2)
(2)
где 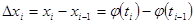 (3)
(3)
|
|
Дата добавления: 2014-01-04; Просмотров: 398; Нарушение авторских прав?; Мы поможем в написании вашей работы!