Властивості спряженого оператора

Лінійні оператори в евклідовому просторі

Позначимо за U_n унітарний (комплексний) лінійний простір, а за А лінійний оператор даного простору.

Лінійний оператор А* називається спряженим до оператора А, якщо виконується умова (Ах, у) = (х, А*у), для будь яких х,у є U_n.

Означення. Лінійний оператор А, що діє в просторі U_n називається самоспряженим якщо виконується умова А = А*.

Означення. Лінійний оператор U, що діє в просторі U_n називається унітарним якщо виконується умова (Ux, Uy) = (x, y), для будь-яких х, у є U_n.

1) (A*)* = A

2) (A·B)* = B*·A*

3) (A+B)* = A*+B*

4) (αA)* = αA*

5) (A-1)* = (A*)-1, |A| ≠ 0

Оператори А і А* називають взаємоспряженими.

Теорема (про повноту векторів самоспряженого оператора). Для будь-якого самоспряженого оператора існує ортогональний базис складений з його власних векторів.

Висновки:

1) Будь-який самоспряжений оператор є оператором простої структури. Для нього існує ортогонормований базис, що складається з власних векторів.

2) Самоспряжений оператор має дійсні власні значення.

3) Симетрична матриця є матрицею самоспряженого оператора в n-вимірному евклідовому просторі і вона є діагоналізованою.

4) Щоб знайти ортогональну матрицю Т, що діагоналізує симетричну матрицю А порядку n треба знайти n ортогональних власних векторів матриці А при чому координати йотого нормованого власного вектора матриці А утворюють йотий стовпець матриці переходу Т.

5) Матриця переходу від одного ортонормованого базису до іншого ортонормованого базису ортогональна.

Виконується умова (2) Т^-1 = Т^тр.

Перевірка діагоналізованої матриці виконується за формулою (1), при чому A’ = diag(λ₁, λ₂, … λ_n).

Приклад. Лінійний оператор А діє в Е у базисі β(e₁’, e₂’, e₃’) має матрицю:

1 1 3

A_β = 0 5 -1

2 7 -3

e₁’ = e₁+2e₂+e₃

e₂’ = e₁+e₂+2e₃

e₃’ = (e₁, e₂, e₃)

Знайти А* в базисі β’.

1) Позначимо А_β матрицю оператора А в базисі β.

Через А_β* I А_β’* матриці самоспряженого оператора.

Підкреслимо, що базис β’ не є ортонормованим, тобто (e_i’, e_j’) ≠ δ_ij.

2) Випишемо через Т_β->β’ матрицю переходу Т_β’->β^-1

1 1 1

Т_β’->β^-1 = 2 1 1

1 2 0

-2 2 0

Т_β’->β = Т_β->β’^-1 = 1 -1 1

3 -1 -1

3) Знаходимо оператор А в базисі β:

A_β = Т_β’->β^-1A_β’ · T_β’->β

1 1 1 1 1 3 -2 2 0 2 -3 7

A_β = 2 1 1 · 0 5 -1 · 1 -1 1 = 6 -4 6

1 2 0 2 7 -3 3 -1 -1 6 -5 5

4) 2 6 6

A_β* = A_β^т = -3 -4 -5

7 6 5

5) A_β'* = Т_β->β’^-1A_β* Т_β->β' =

-2 2 0 2 6 6 1 1 1 -36 37 -15

= 1 -1 1 -3 -4 -5 2 1 1 = 30 30 14

3 -1 -1 7 6 5 1 2 0 26 27 9

Приклад 2. З’ясувати чи буде ортогональним оператором А, що діє в Е_β заданий в ортонормованому базисі матрицею

- 0

А = 0

0 0 1

Оператор буде ортогональним тоді і тільки тоді коли в ортонормованому базисі його матриця ортогональна, тобто виконується умова

0, i ≠k

1, i = k

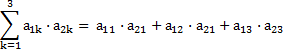
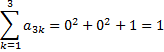
Висновок. Оператор А ортонормований.

Дата добавления: 2014-01-04