Замечание. Расстояние от точки до плоскости остается постоянным при любых на любых движениях жесткой системы

Лемма 2

Расстояние от точки 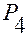до плоскости 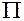остается постоянным при любых на любых движениях жесткой системы.

Ориентация точки 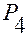относительно плоскости 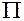остается неизменной при любых и любых движениях жесткой системы.

Поясним, что понимается под ориентацией точки 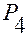относительно плоскости .

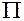Обозначим

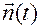— нормаль к плоскости 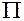в любой момент времени .

Определим ее направление вектором , задаваемым по формуле:

.

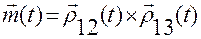Очевидно, в любой момент времени вектор ортогонален плоскости 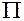, проходящей через точки 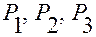(см. рис. 3.1.2).

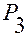
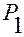
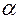
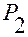
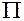
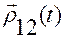
Рис. 3.1.2

Под ориентацией плоскости 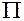понимается направление орта нормали

.

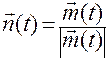Здесь

,

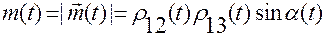где

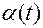— угол между векторам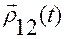и и .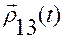

На любом движении имеем:

· согласно уравнениям связей,

, ;

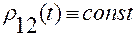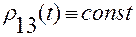· согласно лемме 1,

;

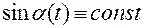· поскольку точки 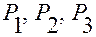не находятся на одной
прямой, то

.

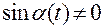Поэтому

.

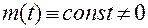Следовательно, вектор 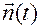может быть вычислен на любом заданном движении жесткой системы в любой момент времени .

Он определяет положительное и отрицательное полупространства относительно плоскости 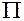в соответствии с неравенствами:

– для любой точки 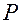, находящейся в положительном полупространстве, выполняется

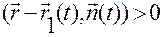; (3.1.1)

– для любой точки 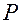, находящейся в отрицательном полупространстве, выполняется

. (3.1.2)

Здесь:

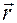· — положение точки 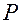, взятой произвольно в
абсолютном пространстве в момент времени ,

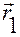· — положение фиксированной нами точки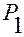
жесткой системы в момент времени ; через точку 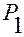проходит плоскость 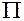в любой момент времени .

Будем говорить, что:

Точка 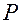имеет положительную (отрицательную) ориентацию по отношению к плоскости 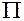в момент времени , если выполняется неравенство (3.1.1) (неравенство (3.1.2)). Точка 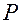имеет нулевую ориентацию, если она находится в плоскости 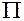, т.е. выполняется равенство

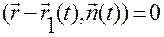. (3.1.3)

Таким образом, лемма 2 утверждает, что ориентация
точки 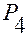по отношению к плоскости 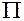сохраняется при любых , т.е. если в некоторый момент выполняется одно из условий (3.1.1), (3.1.2), (3.1.3) для вектора

,

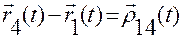то это же самое условие будет выполняться и в любой другой момент времени (независимо от того, какое движение совершает жесткая механическая система).

Дата добавления: 2014-01-04