Доказательство. Теорема существования связанной системы координат

Теорема

Теорема существования связанной системы координат

Докажем следующую теорему.

Для любой жесткой механической системы можно указать декартовую прямоугольную систему координат, в которой все точки механической системы сохраняют значения своих координат неизменными при любых ее движениях.

Если механическая система содержит хотя бы три точки, не лежащие на одной прямой в какой-либо фиксированный момент времени , то, согласно лемме 1, они не будут находиться на одной прямой в любой момент времени на любых движениях этой системы.

Тогда справедливы условия леммы 2, и можно ввести следующую систему координат.

Начало ее в любой момент времени совпадает с точкой 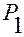, а базис совпадает с ортами 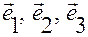, построенными при доказательстве леммы 2.

Заметим, что эта система координат при движении механической системы в общем случае изменяет свое положение в абсолютном пространстве вместе с точками 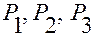, поскольку:

· меняет свое положение ее полюс ,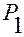

· меняют направления базисные векторы .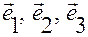

Как следует из доказательства леммы 2, введенная таким образом система координат удовлетворяет условиям теоремы.

Рассмотрим теперь другую ситуацию.

Пусть механическая система состоит из точек, лежащих на одной прямой в некоторый момент времени .

Согласно следствию из леммы 1, все ее точки будут находиться на одной прямой, и их ориентация относительно друг друга будет сохраняться на любых движениях при всех .

Строим систему координат следующим образом:

– полюс ее фиксируем в точке 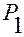указанной прямой;

– в качестве базисного орта 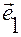берем направляющий вектор
прямой;

– два других базисных орта 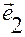и 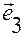выбираем взаимно
ортогональными и ортогональными орту 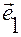так, чтобы
тройка векторов 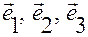была правой.

Тогда для любой точки механической системы можем записать

,

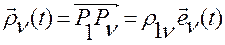где 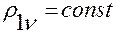— расстояние от точки до точки ;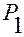

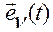— орт, коллинеарный орту 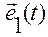, направленный из точки 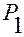в точку .

Из леммы 1 вытекает, что если 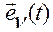совпадает (противоположно направлен) с 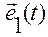в какой-либо момент времени , то и в любой момент времени он будет совпадать (противоположно направлен) с .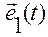

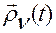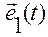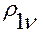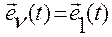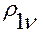Это доказывает, что вектор для любого имеет постоянную проекцию на , равную при (-при 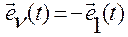), а также то, что 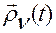ортогонален ортам 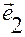и 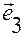. Теорема доказана полностью.

Дата добавления: 2014-01-04