
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение 1. Способы задания движения твердого тела
|
|
|
|
Способы задания движения твердого тела
1º. Векторный способ задания движения твердого тела
В соответствии с понятием движения системы материальных точек (см. определение 4 в §4 Введения) дадим следующее определение движения твердого тела.
Движением твердого тела на промежутке времени  будем называть совокупность вектор-функций, состоящую из движений
будем называть совокупность вектор-функций, состоящую из движений  на этом промежутке всех его точек.
на этом промежутке всех его точек.
Движение твердого тела считается заданным, если описан алгоритм, по которому может быть построено движение любой его точки.
Пусть  — точка твердого тела,
— точка твердого тела, 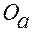 — точка отсчета в абсолютном пространстве,
— точка отсчета в абсолютном пространстве,  — положение точки
— положение точки  в абсолютном пространстве относительно точки
в абсолютном пространстве относительно точки 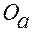 в некоторый момент времени
в некоторый момент времени  (см. рис. 3.2.1).
(см. рис. 3.2.1).
Пусть 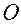 — полюс связанной системы координат,
— полюс связанной системы координат, 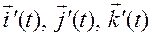 — ее ортонормированный базис. Указанная система координат определяет (задает) пространство, движущееся вместе с твердым телом.
— ее ортонормированный базис. Указанная система координат определяет (задает) пространство, движущееся вместе с твердым телом.
В нем (в указанном пространстве) все точки твердого тела находятся в покое независимо от того, какие движения они совершают в абсолютном пространстве.










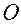






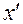
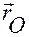


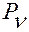










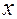 Рис. 3.2.1
Рис. 3.2.1
Другими словами, если обозначим
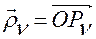 — радиус-вектор точки
— радиус-вектор точки  относительно
относительно
полюса 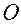 ,
,
 — ее координаты в связанной системе,
— ее координаты в связанной системе,
то положение  в этой системе можно вычислить по формуле
в этой системе можно вычислить по формуле
 .
.
Величины  являются постоянными при всех
являются постоянными при всех  на любых движениях точки
на любых движениях точки  .
.
Если обозначим 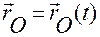 — положение точки
— положение точки 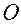 относительно точки отсчета
относительно точки отсчета 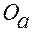 в момент времени
в момент времени  , то положение
, то положение 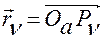 точки
точки  в этот момент можно представить в виде суммы двух векторов:
в этот момент можно представить в виде суммы двух векторов:
· вектора 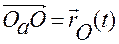 , задающего положение точки
, задающего положение точки 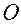 относительно точки отсчета
относительно точки отсчета 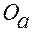 ,
,
· вектора 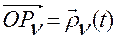 , соответствующего положению точки
, соответствующего положению точки  относительно точки отсчета
относительно точки отсчета 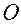 .
.
Таким образом, по правилу сложения векторов можем записать  , или иначе,
, или иначе,
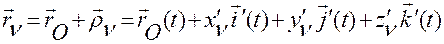 . (3.2.1)
. (3.2.1)
Поскольку в (3.2.1) величины  постоянны, то их можно считать известными для каждой точки
постоянны, то их можно считать известными для каждой точки  твердого тела.
твердого тела.
Они являются координатами точки  в связанной системе, не зависят от движения твердого тела в абсолютном пространстве и могут быть вычислены заранее (до начала его движения).
в связанной системе, не зависят от движения твердого тела в абсолютном пространстве и могут быть вычислены заранее (до начала его движения).
А тогда, если известны законы изменения по времени четырех векторов 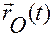 ,
, 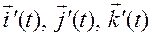 , то соотношение (3.2.1) позволяет вычислить движение
, то соотношение (3.2.1) позволяет вычислить движение  любой точки
любой точки  твердого тела по заданным ее координатам
твердого тела по заданным ее координатам  в связанной системе.
в связанной системе.
Отсюда делаем заключение.
Для определения движения твердого тела на промежутке времени  достаточно задать дважды непрерывно дифференцируемые на этом промежутке времени вектор-функции
достаточно задать дважды непрерывно дифференцируемые на этом промежутке времени вектор-функции
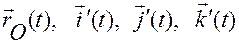 .
.
Если указанные функции заданы, то движение точки  твердого тела, имеющей геометрические характеристики
твердого тела, имеющей геометрические характеристики  , будет определяться соотношением (3.2.1)
, будет определяться соотношением (3.2.1)
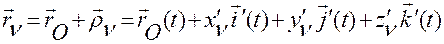 . (3.2.1)
. (3.2.1)
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 372; Нарушение авторских прав?; Мы поможем в написании вашей работы!