Связанная система координат

В этом параграфе показывается существование такой системы координат, в которой координаты любой точки жесткой системы остаются постоянными при любых ее движениях.

Доказательство проводится на основе анализа уравнений связи , которым подчиняются любые две точк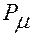и и твердого тела.

1º. Анализ взаимного расположения
точек жесткой системы при ее движении

1.1. Свойства вектор-функций, определяющих взаимное
расположение двух точек при их движении

Пусть 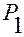и — две фиксированные точки жесткой системы.

Обозначим 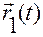и 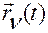— положения этих точек относительно выбранной точки отсчет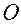а , а 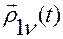— их разность (см. рис. 3.1.1).

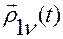
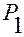
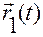
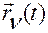
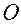
Рис. 3.1.1

В соответствии с понятием положения точки относительно точки 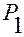вектор 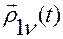задает их взаимное расположение, поскольку — это радиус-вектор точки относительно точки 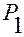в момент времени .

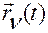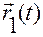Очевидно, он может быть вычислен через положения точки и точки 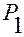по формуле:

.

Обозначим 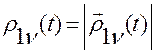— расстояние от точки 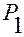до точки в момент времени , 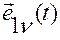— орт направления из точки 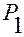в точку ,

.

Так как механическая система является жесткой, то для всех и на любых движениях механической системы выполняются следующие свойства характеристик, определяющих взаимное расположение двух точек:

1) , ;

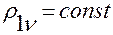2) 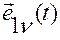— дважды непрерывно дифференцируемая вектор-функция времени так же, как и вектор-функция ;

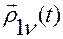3) если известны вектор-функция 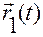и вектор-функция 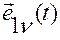, то положение точки относительно точки 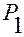по этим функциям определяется по формуле

,

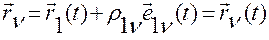где — постоянная величина, которая может быть вычислена независимо от движения жесткой системы.

1.2. Анализ взаимного расположения трех точек
при движении жесткой системы

Пусть заданы три фиксированные точки 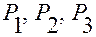жесткой системы. Обозначим

, ,

, ,

, .

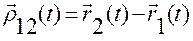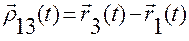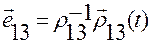Дата добавления: 2014-01-04