Метод множителей Лагранжа.

Чтобы найти условный экстремум функции 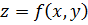при наличии одного уравнения связи 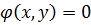составим функцию Лагранжа:

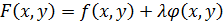
где l - неопределенный постоянный множитель. Затем находят экстремум функции . Необходимые условия экстремума для 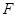выражаются следующей системой трех уравнений с тремя неизвестным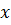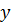и , и .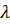

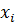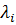Решив эту систему, находят значения , и . Вопрос о существовании и характере условного экстремума в этом случае решается на основе теоремы 2. Для этого исследуется определитель 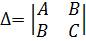, где , , 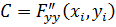. Если при 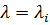, то функция , а, следовательно, и функция 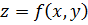имеет в точке 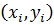при максимум, при 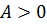- минимум. Если же 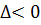, то точка 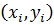не является точкой экстремума. В случае вопрос о существовании экстремума остается открытым. Аналогично находится экстремум при наличии нескольких уравнений связи. Если, например, требуется найти экстремум функции 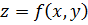при нескольких уравнениях связи

то вводится функция Лагранжа вида

Затем составляется система из - х уравнений с неизвестными и аналогичным образом находится безусловный экстремум.

Пример 71. Найти условный экстремум функции при условии .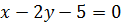

Решение. Способ 1. Из уравнения связи выразим переменную 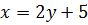и подставим в исходную функцию , получим функцию одной переменной 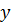, . После преобразования, запишем функцию в виде

.

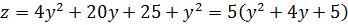Находим производную

Дата добавления: 2014-01-04