Свойства средней арифметической

1. Средняя арифметическая постоянной равна самой постоянной.

2. Если все варианты увеличить (уменьшить) на одно и то же число, то средняя арифметическая увеличится (уменьшится) на то же число

.

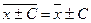3. Если все варианты увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз

.

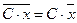4. Сумма отклонений вариантов от их средней арифметической равна нулю

.

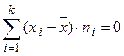5. Средняя арифметическая алгебраической суммы соответствующих друг другу значений нескольких признаков равна алгебраической сумме средних арифметических этих признаков

.

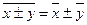6. Если ряд наблюдений состоит из нескольких непересекающихся групп наблюдений, то средняя арифметическая всего ряда наблюдений равна взвешенной средней арифметической групповых средних, причем весами являются объемы групп

,

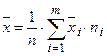где 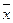− общая средняя, 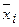− групповая средняя 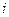-той группы, объем которой равен 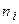, 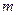− число групп.

7. Если все частоты вариантов умножить на одно и то же число, то средняя арифметическая не изменится.

Определение 13.7. Модой выборочной совокупности называют наиболее часто встречающееся значение признака в данном ряду распределения.

Для дискретного вариационного ряда (ДВР) мода определяется как значение признака с наибольшей частотой. Для интервального вариационного ряда (ИВР) мода может быть определена как значение признака, которому отвечает наибольшая плотность распределения частости.

Если 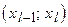– модальный интервал, т.е. интервал, которому соответствует наибольшая частота 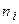, и интервалы вариационного ряда имеют постоянную длину 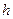, то мода исследуемого признака 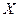вычисляется по формуле

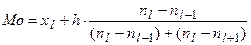, (13.3)

где 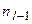и 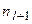– частоты, которые соответствуют предмодальному и послемодальному интервалам.

Определение 13.8. Медианой 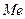выборочной совокупности называется значение признака, относительно которого совокупность делится на две равные по объему части, причем в одной из них содержатся члены, у которых значения признака не больше медианы 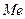, а в другой – члены со значениями признака не меньше .

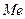Для нахождения медианы в ДВР первоначально сумму частот делят пополам 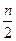. Если сумма частот упорядоченной совокупности нечетна, то порядковым номером требуемого варианта является 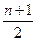. Если сумма частот четна, то в качестве медианы берут значение варианта с номером 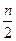или же среднее значений признака с номерам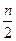и и .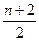

Для ИВР сначала находят медианный интервал 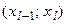, его номер соответствует интервалу, кумулятивная частота которого равна или превышает половину суммы частот. Медиану вычисляют по формуле

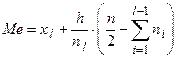, (13.4)

где 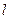– порядковый номер медианного интервала, 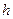– его длина, 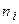– частота медианного интервала.

Пример 13.5. Для ДВР примера 13.3 – распределения сотрудников фирмы по количеству членов в семье – найти среднюю арифметическую, моду и медиану.

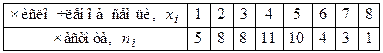
Решение. 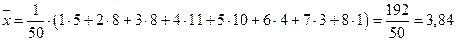(чел.),

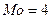(чел.), так как варианте 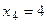соответствует наибольшая частота 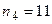, 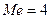(чел.), так как в упорядоченной по возрастанию совокупности 25-й и 26-й члены принимают значение 4.

Ответ. 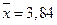(чел.), 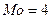(чел.), 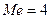(чел.).

Пример 13.6. Для ИВР примера 13.4 – распределения дневной выручки – найти среднюю арифметическую, моду и медиану.

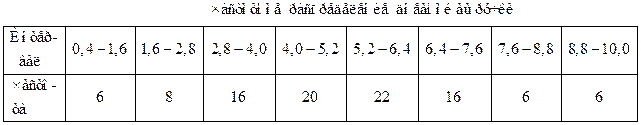
Решение. Для вычисления указанных числовых характеристик перейдем к ДВР, заменив интервалы их серединными значениями, и для полученного ряда найдем требуемые характеристики. Результаты вычисления средней арифметической представим во вспомогательной таблице 13.4.

Тогда 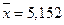(млн.ден.ед.).

Так как наибольшая частота 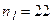соответствует интервалу 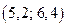, то 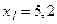, , 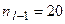, 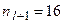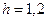и по формуле (13.3):

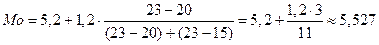(млн. ден.ед.).

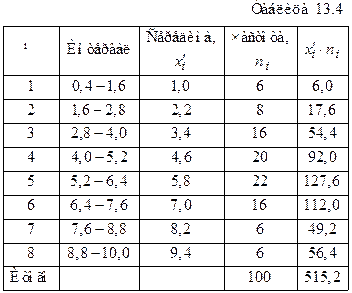
Так как порядковый номер медианного интервала 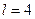, то на основании формулы (13.4) получим

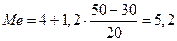(млн.ден.ед.).

Ответ. 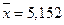(млн.ден.ед.), 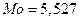(млн.ден.ед.), 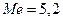(млн.ден.ед.).

Дата добавления: 2014-01-04