Начальные и центральные моменты вариационного ряда

Средняя арифметическая и дисперсия вариационного ряда являются частными случаями более общего понятия – моментов вариационного ряда.

Определение 13.11. Начальным выборочным моментом 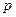-го порядка называется средняя арифметическая 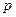степеней наблюдаемых значений признака 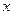, т.е.

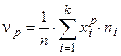. (13.9)

По определению, 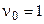, – средняя арифметическая является начальным моментом первого порядка вариационного ряда, 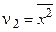, и т.д.

Определение 13.12. Центральным выборочным моментом 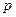-го порядка называется средняя арифметическая 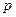степеней отклонений наблюдаемых значений признака 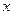от его среднего арифметического, т.е.

. (13.10)

По определению, , , 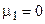, 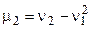причем центральный момент второго порядка является дисперсией вариационного ряда.

Определение 13.13. Выборочным коэффициентом асимметрии вариационного ряда называется число 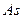, определяемое формулой

. (13.11)

Выборочный коэффициент асимметрии служит для характеристики асимметрии полигона вариационного ряда. Если , то распределение имеет симметричную форму, т.е. варианты, равноудаленные от 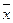, имеют одинаковую частоту. Если полигон асимметричен, то одна из ветвей его, начиная с вершины, имеет более пологий «спуск», чем другая. В случае 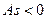более пологий «спуск» полигона наблюдается слева, в этом случае асимметрию называют левосторонней. В случае 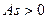пологий «спуск» полигона наблюдается справа, асимметрия правосторонняя.

Определение 13.14. Выборочным эксцессом вариационного ряда называется число , определяемое формулой

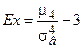. (13.12)

Выборочный эксцесс служит для сравнения на «крутость» выборочного распределения с нормальным распределением. Если выборочному распределению соответствует, то соответствующий полигон имеет более пологую вершину по сравнению с нормальной кривой. В случае полигон более крутой по сравнению с нормальной кривой.

Пример 13.5 (продолжение). Найти коэффициент асимметрии и эксцесс ДВР примера 13.3 – распределения сотрудников фирмы по количеству членов в семье.

Решение. Ранее были вычислены средняя арифметическая 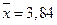(чел.) и СКО 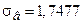(чел.). Для вычисления центральных моментов третьего и четвертого порядков на основе таблицы 13.5 составим вспомогательную таблицу 13.7.

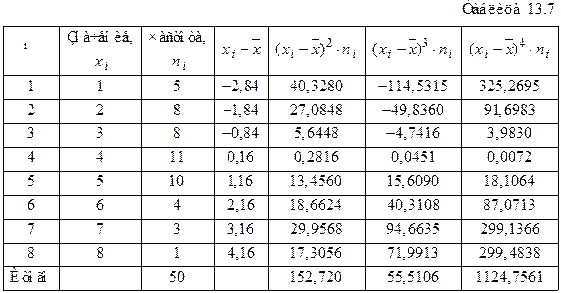
Тогда , ,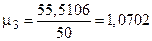

, .

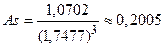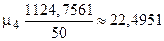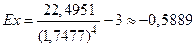Ответ. , .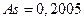

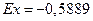Пример 13.6 (продолжение). Найти коэффициент асимметрии и эксцесс ИВР примера 13.4 – распределения дневной выручки.

Решение. Ранее были вычислены средняя арифметическая 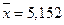(млн.ден.ед.) и СКО (млн.ден.ед.). Для вычисления центральных моментов третьего и четвертого порядков на основе таблицы 13.6 составим вспомогательную таблицу 13.8. Тогда

, ,

, .

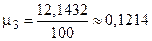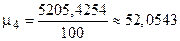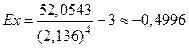Ответ. , .

Замечание 13.2. Для нормального распределения признака 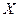график функции плотности будет симметричен по отношению к прямо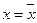й и , .

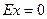Согласно приведенным определениям можно выделить три вида числовых характеристик вариационного ряда:

– меры положения частотного распределения наблюдаемых значений признака : , , ;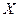

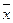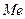– меры вариации – измеряют количественную величину рассеивания вокруг мер положения: 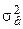и ;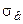

– меры формы частотного распределения: 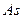и .

Дата добавления: 2014-01-04