Упражнения. Определение ранга матрицы через миноры

Определение ранга матрицы через миноры.

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

(ПРОДОЛЖЕНИЕ)

Определение. Будем говорить, что для (m,n)- матрицы А

ранг rk A= r, если все миноры в А порядка (r+1) равны нулю, и существует минор порядка r, который не равен нулю.

1. Доказать, что если rk A = r, то все миноры в А порядка s, s > (r+1), равны нулю.

2. Доказать, что rk A = 0 Û A = 0.

3. Доказать, что rk A = 1 Û в А $ ненулевая строка, а все остальные строки ей пропорциональны.

Далее мы докажем, что rk A = rg A.

Утверждение. Если А – (m,n) -матрица, и А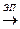А¢, то rk A¢ £ rk A.

Доказательство. Пусть rk A= r. Покажем, что в матрице А¢ все миноры М¢_r+1 порядка r+1 равны нулю. Отсюда и будет следовать утверждение.

Пусть АА¢, и i- я строка матрицы А¢ получается сложением i- й строки матрицы А с j- й строкой, умноженной на сÎ Р (j¹ i). Рассмотрим минор М¢_r+1 порядка r+1 в А¢. Если i- я строка матрицы А¢ не входит в М¢_r+1, то минор М¢_r+1 равен соответствующему минору М_r+1 матрицы А: М¢_r+1= М_r+1= 0. Если в М¢_r+1 входят и i- я и j- я строки матрицы А¢, то минор М¢_r+1 получается из соответствующего минора М_r+1 с помощью ЭП-I, то есть М¢_r+1= М_r+1= 0. Если же i- я строка матрицы А¢ входит в М¢_r+1, а j- я строка матрицы А¢ не входит в М¢_r+1, то М¢_r+1= М_r+1± с М⁰_r+1,= 0± с0 = 0, где М_r+1 и М⁰_r+1 – соответствующие миноры матрицы А.

Пусть теперь А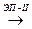А¢, и при ЭП-II в матрице А меняются местами i -я и j -я строки. Если i- я и j- я строки матрицы А¢ не входят в М¢_r+1, то М¢_r+1= М_r+1= 0. Если i- я и j- я строки матрицы А¢ входят в М¢_r+1, то М¢_r+1= - М_r+1= - 0 = 0. Если же i- я строка матрицы А¢ входит в М¢_r+1, а j- я строка матрицы А¢ не входит в М¢_r+1, то М¢_r+1=± М⁰_r+1 = 0, где М⁰_r+1 - некоторый минор матрицы А.

Наконец, пусть А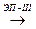А¢, и при ЭП-III в матрице А i- я строка умножается на сÎ Р, с ¹ 0. Если i- я строка матрицы А¢ не входит в М¢_r+1, то М¢_r+1= М_r+1= 0. Если же i- я строка матрицы А¢ входит в М¢_r+1, то М¢_r+1= с М_r+1=с 0 = 0.

ÿ

Следствие. Если А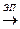А¢, то rk A¢ = rk A.

Доказательство. Так как А А¢, то А¢ А, причем обратное ЭП - того же типа (см. упражнение 1 из 4.2). Следовательно, rk A¢ £ rk A, и rk A £ rk A¢, то есть rk A¢ = rk A.

ÿ

С помощью элементарных преобразований (как в 4.2) приведем матрицу А к ступенчатому виду

= .

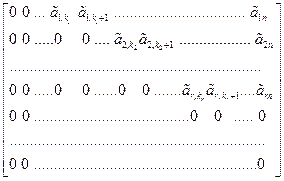Тогда rk A = rk .

Утверждение. rk = r = rg = rg A.

Доказательство. Так как в существуют лишь r ненулевых строк, то любой минор порядка r+1 содержит нулевую строку и поэтому равен нулю. Кроме того, очевидно, минор r -го порядка, стоящий на пересечении первых r строк и столбцов с номерами k₁, k₂,…, k_r, не равен нулю – он равен 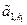××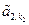…×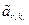¹ 0.

ÿ

Итак, мы доказали, что rk A = rg A. Далее для ранга матрицы мы будем использовать единое обозначение rg A.

Утверждение. rg A^t = rg A.

Доказательство. Так как определитель не меняется при транспонировании матрицы, то rk A^t = rk A, и rg A^t = rk A^t = rk A = rg A.

ÿ

Последнее утверждение означает, что ранги матрицы по строкам и по столбцам совпадают, то есть размерность линейной оболочки строк матрицы и размерность линейной оболочки столбцов матрицы одинаковы.

Дата добавления: 2014-01-04