Решение систем линейных уравнений (продолжение)

Запишем систему линейных уравнений (4.1) в виде

S: .

И рассмотрим систему

S¢: .

Очевидно, S¢ Þ S, и если уравнение F = 0 является следствием системы S, то S Þ S¢, и S Û S¢. Более того, S Û S¢ тогда и только тогда, когда уравнение F = 0 является следствием системы S. Это означает, что добавление к системе S или удаление из системы S¢ уравнения, которое является следствием системы S, не меняет множества решений системы S. Чтобы сделать систему проще, естественно удалять из системы все уравнения, которые являются следствиями остальных уравнений.

Утверждение. Если F = a₁F₁+a₂F₂+…+a_mF_m, то уравнение F = 0 является следствием системы S, и S¢ Û S.

Доказательство очевидно: любое решение системы S обращает в 0 все F₁, F₂,…, F_m, и значит, обращает в 0 выражение F, так как a₁0 +a₂0+…+a_m0 = 0.

ÿ

Посмотрим, когда существуют такие a₁, a₂, …,a_m, что a₁F₁+a₂F₂+…+a_mF_m=F. Если такие a₁,a₂, …,a_m существуют, то, сравнивая коэффициенты при х₁, х₂,…, х_п и правые части уравнений, получим, что a₁, a₂, …,a_m являются решениями следующей системы из п+1 уравнений:

Q: .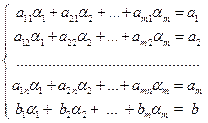

Наоборот, если a₁, a₂ , …, a_m - решения этой системы, то a₁F₁+a₂F₂+…+a_mF_m = F. Таким образом, F = a₁F₁+…+a_mF_m Û существует решение системы Q Û (по теореме Кронекера-Капелли) равны ранги матриц

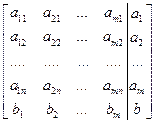и 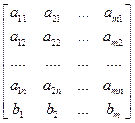, или равны ранги транспонированных матриц

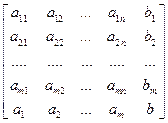и .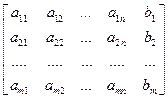

Следовательно, если ранги этих матриц равны, то последнее уравнение в системе S¢ можно отбросить и перейти от системы S¢ к системе S.

Предположим теперь, что нам дана СЛУ (4.1), у которой ранг основной матрицы и ранг расширенной матрицы равны r (то есть система совместна). Для простоты будем считать, что отличный от нуля минор M_r порядка r находится в левом верхнем углу матрицы А. Тогда все уравнения, начиная с (r+1)- го и до т- го, являются линейными комбинациями первых r уравнений, и значит, их следствиями. То есть наша СЛУ равносильна системе из первых r уравнений, а уравнения с (r+1)- го и до т- го мы можем отбросить. Оставшиеся r уравнений мы запишем в виде

.

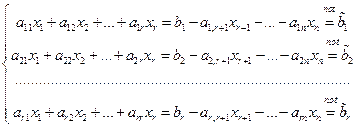Так как определитель основной матрицы этой системы равен M_r ¹ 0, то, решая эту систему по Крамеру, получим х_i=/M_r, i= 1,…,r, где - определители, зависящие от х_j, j= r+1,…,n. Раскрывая эти определители, пользуясь линейностью по i -му столбцу, получим: =D_i + с_i,r+1 х_r+1+…+ с_i,nх_n, i=1,…,r. Подставляя эти формулы в х_i=/M_r, получим выражения главных неизвестных через свободные.

Лекция 17.

8.3. Необходимые и достаточные условия равенства нулю определи­теля.

Теорема. Пусть А – (п,п)- матрица. Тогда равносильны следующие условия:

1. det A = 0,
2. rg A < n,
3. однородная СЛУ с основной матрицей А имеет ненулевое решение,
4. столбцы матрицы А линейно зависимы,
5. строки матрицы А линейно зависимы.

Доказательство. Из определения ранга rk 1 Û 2. Если det A ¹ 0, то, например, по правилу Крамера существует только нулевое решение однородной СЛУ с основной матрицей A. Наоборот, если det A = 0, rg A = r < n, то у однородной СЛУ существуют n – r свободных неизвестных (см. 4.3), и, значит, существует ненулевое решение. Отсюда 1 Û 3. Далее, существование ненулевого решения для однородной СЛУ равносильно линейной зависимости вектор-столбцов матрицы А (см. 7.5), то есть 3 Û 4. Так как det A = det A^Т, то 1 Û 5.

ÿ

Дата добавления: 2014-01-04