
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоретическая механика. Статика. 3. Пространственная система сил
|
|
|
|
Лекция 2.
План занятия:
1. Плоская система сил
2. Плоские формы
3. Пространственная система сил
4. Центр тяжести
Перенос силы из одной точки в другую называют приведением силы к данной точке. Сила Р" называется приведенной силой, а пара (Р'Р) присоединенной парой. Ее момент
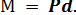
Систему сил в плоскости можно привести к одной силе, приложенной в произвольно выбранной точке, Эта сила R называется главным вектором всей системы сил.
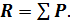 (1)
(1)
Кроме нее, получится одна пара, момент которой равен сумме моментов сил системы относительно центра приведения и который называется главным моментом данной системы сил относительно этого центра.
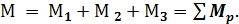 (2)
(2)
Чтобы привести систему сил в равновесие, необходимо:
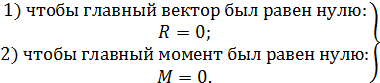 (3)
(3)
Три уравнения равновесия системы сил, произвольно расположенных на плоскости:
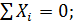 (4)
(4)
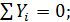 (5)
(5)
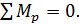 (6)
(6)
Отсюда можно сделать следующее заключение: если твердое тело под действием плоской системы сил находится в равновесии, то:
1) Сумма проекций всех сил на ось x равна нулю (силы не перемещают тело вдоль оси x);
2) Сумма проекций всех сил на ось y равна нулю (силы не перемещают тело вдоль оси y);
3) Сумма моментов всех сил относительно любой точки равна нулю (тело не может вращаться).
Фермой называется жесткое сооружение, состоящее из прямолинейных стержней, соединенных между собой шарнирами. В такой конструкции стержни могут испытывать только растяжение или сжатие.
Места соединения жестких стержней или звеньев называют узлами.
Число шарниров в каждом стержне может быть различное, но не меньше двух.
Основные элементы фермы носят следующие названия:
1. Расстояние между опорами называется пролетом фермы.
2. Цепь звеньев, расположенных по внешнему контуру фермы, образует верхний пояс и нижний пояс.
3. Вертикальные стержни, соединяющие верхний и нижний поясы, называются стойками, а наклонные стержни — раскосами.
Чтобы стержни фермы работали только на растяжение или сжатие, необходимо соблюсти следующие условия:
1) стержни в узлах должны соединяться шарнирами без трения;
2) все силы, действующие на ферму, должны быть приложены только в узлах фермы.
Когда к одной точке твердого тела приложено несколько сил, расположенных в различных плоскостях, то такая система сил называется пространственной системой
При трех силах, сходящихся в одной точке и действующих в разных плоскостях, равнодействующая их выражается диагональю параллелепипеда, построенного на этих силах.
1) Проекция силы P на ось x: 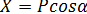
2) Проекция силы P на ось y: 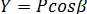
3) Проекция силы P на ось z: 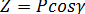
Тогда величина силы P определится по формуле
 (7)
(7)
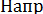 авление силы P определится из равенств:
авление силы P определится из равенств:
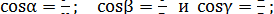 (8)
(8)
Моментом силы относительно оси называется момент проекции этой силы на плоскость, перпендикулярную к оси, относительно точки пересечения оси с плоскостью.
Момент силы относительно оси может быть равен нулю в двух случаях:
1) когда сила Р параллельна оси (в этом случае 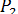 = 0);
= 0);
2) когда линия действия силы Р пересекает ось (в этом случае h = 0).
Равновесие твердого тела, находящегося под действием сил, произвольно расположенных в пространстве, возможно, если удовлетворяются следующие шесть уравнений:
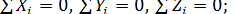 (9)
(9)
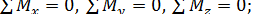 (10)
(10)
Равнодействующая сила тяжести всех частиц тела называется весом тела.
Эта равнодействующая приложена в центре всей системы параллельных сил, который называется центром тяжести.


Пусть даны три параллельные силы 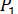 ,
, 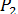
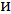
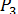 , направленные в одну и ту же сторону и приложенные в точках
, направленные в одну и ту же сторону и приложенные в точках 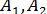
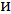
 (рис. 1).
(рис. 1).
Положение точки А1 определяется координатами х1,y1, z1, точки A2 — координатами х2,y2,z2, точки A3 — координатами х3,y3,z3, а положение центра С параллельных сил определяется координатами хс, ус, zc.
Составив моменты всех сил относительно трех осей, напишем, что момент равнодействующей равен алгебраической сумме моментов составляющих сил, т. е.
Rxc = Р1х1 + Р2х2 + Р3х3;
Ryc = Р1y1 + Р2y2 + Р3y3;
Rzc = Р1z1 + Р2z2 + Р3z3;
Отсюда находим искомые координаты точки С приложения равнодействующей силы:
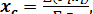 (11)
(11)
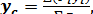 (12)
(12)
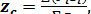 (13)
(13)
По этим формулам определяются координаты центра параллельных сил.
1. Центр тяжести прямолинейного однородного стержня АВ, имеющего постоянное сечение, находится на середине этого стержня.
2. Центр тяжести ломаной линии (рис. 2, а), состоящей из отрезков АВ и ВС, определяется следующим путем:
а) вначале отмечаем центры тяжести С1 и С2 в серединах отрезков АВ и ВС;
б) затем прикладываем в точках С1 и С2 веса G1 и G2 отрезков АВ и ВС, пропорциональные их длинам;
в) для определения общего центра тяжести ломаной линии ABC соединяем прямой точки С1 и С 2 и, пишем равенство моментов G1• С1С, находим на этой прямой центр С двух параллельных сил G1 и G2. Точка С и будет являться центром тяжести ломаной линии ABC, а,вес ее будет G = G1 + G2 и будет приложен в этой точке С.
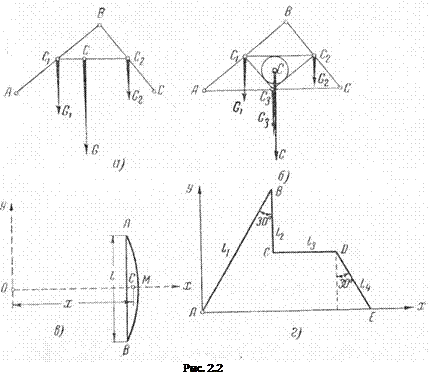 |
3. Центр тяжести периметра треугольника ABC (рис. 2,б) расположен в центре круга, вписанного в треугольник С1 C2C3, составленный из прямых С1 C2, С2С3 и С3С1 соединяющих точки С1, С 2 и С 3 центров тяжести сторон треугольника ABC.
4. Центр тяжести периметра параллелограмма расположен в точке пересечения его диагоналей.
5. Центр тяжести дуги окружности. Для определения положения центра тяжести дуги окружности (рис. 2, в) проводим из ее центра О линию симметрии ОМ, на которой и будет находиться центр тяжести дуги АМВ. Расстояние от точки С центра тяжести дуги окружности до ее центра определяется по формуле
 ; (14)
; (14)
где l — длина хорды АВ;
b—» дуги АМВ;
r— радиус окружности.
Для дуги, равной половине окружности,
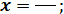
Для четверти окружности

Для шестой части окружности
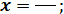
6. Определение центра тяжести ломаной линии ABCD(рис 2, г) производится с помощью формул:
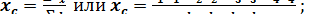 (15)
(15)
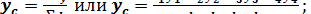 (16)
(16)
аналогичных формулам (47) и (48).
Здесь 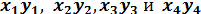 — координаты центров тяжести отрезков
— координаты центров тяжести отрезков 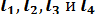 .
.
1. Центр тяжести площади треугольника находится в точке пересечения его медиан. Если 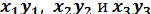 — координаты вершин треугольника, то координаты центра тяжести С могут быть определены по формулам:
— координаты вершин треугольника, то координаты центра тяжести С могут быть определены по формулам:
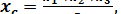
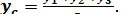 (17)
(17)
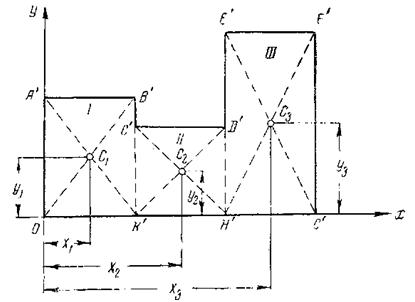
Рис. 2.3
Доказательство. Разобьем площадь треугольника на узкие полоски линиями, параллельными его основанию. Считая приближенно такую полоску за прямую линию (это представление будет тем точнее, чем уже полоска), утверждаем, что центр тяжести полоски лежит в ее середине. Геометрическое место середин всех таких полосок есть медиана треугольника. Разбивая площадь треугольника на полосы, параллельные другой его стороне, находим, что центр тяжести лежит и на второй медиане. Следовательно, он лежит в точке их пересечения.
2. Центр тяжести площади сложной фигуры.Пусть дана площадь OA'B'C'D'E'F'C'O(рис. 3), требуется определить ее центр тяжести. Разобьем фигуру на три прямоугольника — I, II и III, Центрытяжести которых расположены в точках С 1, С 2 и С 3 пересечения диагоналей этих прямоугольников.
Обозначим координаты центра тяжести С 1, С 2 и С 3 через 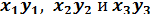 ,тогда координаты центра тяжести всей площади можно определить по формулам:
,тогда координаты центра тяжести всей площади можно определить по формулам:
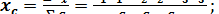 (18)
(18)
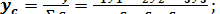 (19)
(19)
где S 1, S 2 и S 3 – площади прямоугольников I, II и III.
Формулы для опрееления центра тяжести объема:
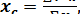 (20)
(20)
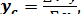 (21)
(21)
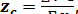 (22)
(22)
1) у призмы и цилиндра центр тяжести находится на середине оси симметрии, проходящей через центры тяжести оснований этих фигур;
2) у пирамиды и конуса центр тяжести расположен на прямой линии, соединяющей вершину с центром тяжести основания, и удален от этого основания на 1/4 всей длины прямой линии.
Если твердое тело соприкасается с горизонтальной плоскостью или с поверхностью в одной точке, то равновесие тела будет в том случае, когда центр тяжести его лежит на одной вертикали с точкой опоры.
В этом случае имеют место три вида равновесия:
1) устойчивое равновесие;
2) неустойчивое равновесие;
3) безразличное равновесие.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1539; Нарушение авторских прав?; Мы поможем в написании вашей работы!