Структура модели фотона

Поскольку фотон имеет в движении массу 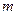, то вполне естественно, что он имеет и центр масс, то есть такую точку, в которую можно свести всю массу фотона и движение этой точки будет характеризовать движение всего фотона. Волновые свойства фотона указывают на то, что эта точка (центр масс) описывает волновую траекторию. Постоянство скорости движения фотонов всех диапазонов указывает на то, что траектории движения центров масс фотонов всех частот - одни и те же. Вполне естественно, что в этом случае и структура фотонов всех частот должна быть одинаковой. Какова эта структура?

Ответ на этот вопрос скрыт в математических моделях, описывающих поведение фотона (49-56) и в физическом смысле фундаментальных констант. Мы уже показали, что радиус 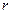вращения фотона, электрона и других частиц равен длинам их волн 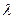. С учетом этого физический смысл постоянной Планка становится предельно ясным 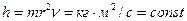- момент количества движения или момент импульса, или кинетический момент кольца. Мы выбираем понятие «Кинетический момент кольца», чтобы подчеркнуть, что законы классической механики успешно работают в микромире [9], [10].

Известно, что постоянством кинетического момента управляет закон сохранения кинетического момента [11]. Он гласит: если сумма моментов внешних сил, действующих на вращающееся тело, равна нулю, то кинетический момент 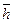этого тела остаётся постоянным по величине и направлению [11].

Нетрудно видеть, что из двух констант 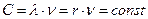и 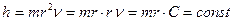автоматически следует третья константа 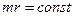. Её размерность 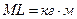. В системе СИ нет величины с такой размерностью, поэтому возникает необходимость ввести название новой константе [12]. Назовём её константой локализации фотона в пространстве и обозначим .

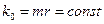В системе СИ величина новой константы равна [1]

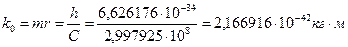(57)

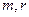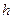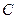Какую же электромагнитную структуру должен иметь фотон, чтобы обеспечивалось такое удивительное сочетание его параметров и , которые меняются в столь широком диапазоне (см. табл. 11, 12, 13) так, что обеспечивается постоянство сразу трех констант , и ?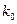

Из константы следует, что фотон имеет форму вращающегося кольца (рис. 9, а), которое движется с постоянной скоростью .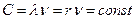

Константой 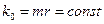управляет закон, который локализует фотон в пространстве. Он гласит: с увеличением массы 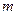фотона его радиус уменьшается пропорционально и наоборот или произведение массы фотона на радиус его кольца – величина постоянная.

Из равенства 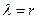следует, что кольцо разделено хордами на шесть частей (рис. 9, b). Это даёт нам основание предположить, что фотон состоит из шести электромагнитных полей, каждое из которых имеет центр масс 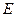(рис. 9, с).

Так как фотон имеет массу и электромагнитную природу, то у нас остаётся одна возможность: считать, что массу фотона формируют шесть его электромагнитных полей. Тогда постоянство трех констант 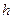, 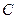и 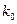должно обеспечиваться равенством электромагнитных сил, генерируемых движущимися электромагнитными полями, и ньютоновскими силами, действующими на центры масс 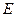этих полей.

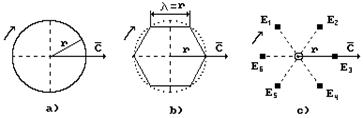
Рис. 9. К выявлению структуры фотона

Электромагнитная природа фотона предопределяет наличие электромагнитных сил, а наличие вращающихся масс - центробежных сил инерции. Из этого следует, что локализацию фотона в пространстве обеспечивают уравновешивающие друг друга электромагнитные и центробежные силы инерции.

Поскольку центробежные силы инерции направлены радиально от центра вращения, то магнитная составляющая электромагнитных сил должна быть направлена также радиально, но только к центру вращения.

Далее, чтобы магнитные силы сжимали фотон, они должны быть направлены радиально к центру. Это возможно, если магнитные поля будут подобны магнитным полям радиально расположенных стержневых магнитов, направленных навстречу друг другу разноименными магнитными полюсами.

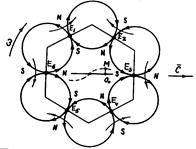
Из изложенного следует схема электромагнитной модели фотона, показанная на рис. 10, а. На рис. 10, b - эта же модель, смоделированная немецким физиком Walter Krauser [13] с помощью постоянных магнитов.

Как видно (рис. 10), модель фотона состоит из шести замкнутых друг с другом магнитных полей, которые при движении модели опоясываются электрическими полями и превращаются в электромагнитные поля. Магнитные поля фотона подобны магнитным полям стержневых магнитов. Векторы напряженности этих магнитных полей, чередуются так, что у противоположных полей они направлены вдоль одного диаметра в одну и ту же сторону, сжимая фотон. Но, так как фотон все время находится в движении, то магнитные силы, сжимающие фотон, уравновешиваются центробежными силами инерции, действующими на центры масс 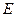электромагнитных полей (рис. 9, с).

a)

b)

Рис. 10. Схемы электромагнитных моделей фотона:

а) теоретической, b) смоделированной

Сложная, конечно, получается модель, но только в этой модели реализуется постоянство констант 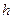, 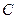и 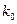, и самое главное - закон сохранения кинетического момента. Реализация эта идет следующим образом.

Известно, что с увеличением массы 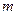(энергии) фотона длина 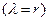его волны уменьшается (табл. 11, 12, 13).Такая закономерность однозначно следует из константы локализации фотона 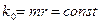. Это же следует и из закона сохранения кинетического момента 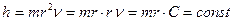. C увеличением массы 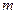фотона растет плотность его электромагнитных полей (рис. 10) и за счет этого увеличиваются электромагнитные силы, сжимающие фотон, которые все время уравновешиваются центробежными силами инерции, действующими на центры масс этих полей. Это приводит к уменьшению радиуса 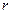вращения фотона, который всегда равен длине его волны 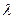. Но поскольку радиус 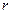в выражении постоянной Планка возводится в квадрат, то для сохранения постоянства постоянной Планка частота 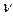колебаний фотона должна при этом увеличиться. В силу этого незначительное изменение массы фотона автоматически изменяет его радиус 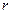вращения и частоту так, что кинетический момент (постоянная Планка) остается постоянным. Таким образом, фотоны всех частот, сохраняя свою электромагнитную структуру, меняют массу, частоту и длину волны так, чтобы 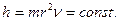То есть принципом этого изменения управляет закон сохранения кинетического момента.

Такой же четкий и ясный ответ мы получаем и на следующий фундаментальный вопрос: почему фотоны всех частот движутся в вакууме с одинаковой скоростью?

Потому что изменением массы 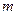фотона и его радиуса 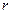управляет закон локализации 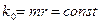фотона. Из него следует, что при увеличении массы 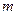фотона его радиус 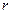уменьшается пропорционально и наоборот. Тогда для сохранения постоянства постоянной Планка 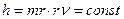(при 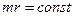) величина 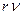также должна быть постоянной. В результате -.

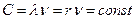Таблица 13. Диапазоны изменения длины волны 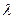и массы 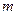электромагнитных излучений

Диапазоны	Длина волны, м	Масса, кг
1. Низкочастотный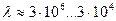
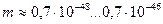
2. Радио
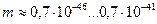
3. Микроволновый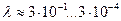
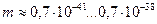
4. Реликтовый (макс)
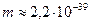
5. Инфракрасный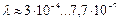
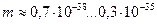
6. Световой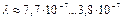
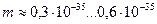
7. Ультрафиолетовый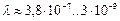
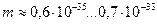
8. Рентгеновский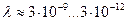
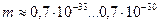
9. Гамма диапазон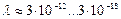

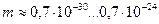
Новая константа 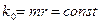позволяет дополнить таблицы 11 и 12 величинами масс фотонов, соответствующих каждому диапазону (табл. 13).

Поскольку структура электромагнитного излучения неизвестна, то фотон, соответствующий максимальной длине волны 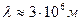этого излучения (табл. 13), должен иметь массу

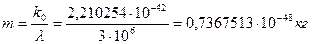. (58)

Тогда фотон, соответствующий гамма диапазону, будет иметь массу

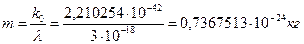(59)

Теперь ясно, что максимальную проницаемость гамма фотона обеспечивает его минимальный размер (радиус 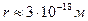) и максимальная масса 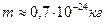. Что же касается фотона с максимальной длиной волны 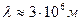и минимальной массой 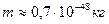, то тут - полная неясность. Трудно представить фотон с радиусом 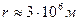, движущийся со скоростью света. Площадь пространства, ограниченная радиусом 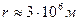, будет равна 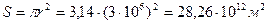. Тогда удельная плотность фотона будет равна

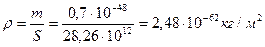(60)

Вряд ли возможно формирование ньютоновских и электромагнитных сил при такой небольшой плотности массы фотона. Поэтому должен существовать предел максимального радиуса 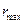и минимальной массы 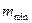фотона. Поиск этого предела – наша следующая задача.

Известно, что фотоны, формирующие спектральные линии, излучают электроны при энергетических переходах в атомах. Из этого следует, что они же формируют и электромагнитные волны. Как они это делают? Ответ на этот вопрос даёт гипотеза Аллана Холдена. Реализация этой гипотезы показана на (рис. 8).

Как видно (рис. 8), электромагнитную волну формируют импульсы единичных фотонов, которые представлены в виде совокупности шариков. Шарики - это фотоны. Расстояние между импульсами фотонов (шариков) равно длине волны электромагнитного излучения, а длина волны каждого отдельного фотона значительно меньше. Она определяет область его локализации в пространстве. Если это так, то величину максимального радиуса 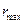, а значит и минимальной массы 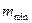фотона можно выявить из анализа спектров атомов.

В табл. 14. приведен спектр атома водорода, включая 150-й энергетический уровень. Современной науке неизвестно, сколько энергетических уровней имеет электрон атома водорода и электроны других атомов, поэтому попытаемся установить это.

Таблица 14. Спектр атома водорода

Номер энергетического уровня, n	Энергия возбуждения (eV)	Энергия связи электрона с ядром (eV)
	-0.00000000000000075	13.59800000000000000
	10.19849999999999872	3.39950000000000000
	12.08711111111111168	1.51088888888888896
	12.74812500000000000	0.84987500000000000
	13.05408000000000000	0.54391999999999992
	13.22027777777777664	0.37772222222222224
	13.32048979591836672	0.27751020408163264
	13.38553125000000000	0.21246875000000000
	13.43012345679012352	0.16787654320987654
	13.46202000000000000	0.13597999999999998
	13.48561983471074304	0.11238016528925620
	13.50356944444444416	0.09443055555555556
	13.51753846153846016	0.08046153846153846
	13.52862244897959168	0.06937755102040816
	13.53756444444444416	0.06043555555555555
	13.54488281249999872	0.05311718750000000
	13.55094809688581376	0.04705190311418685
	13.55603086419753216	0.04196913580246914
	13.56033240997229824	0.03766759002770083
	13.56400500000000000	0.03399500000000000
	13.56716553287981824	0.03083446712018140
	13.56990495867768576	0.02809504132231405
	13.57229489603024384	0.02570510396975426
	13.57439236111110912	0.02360763888888889
	13.57624320000000000	0.02175680000000000
	13.57788461538461440	0.02011538461538462
	13.57934705075445760	0.01865294924554184
	13.58065561224489728	0.01734438775510204
	13.58183115338882304	0.01616884661117717
	13.58289111111111168	0.01510888888888889
	13.58385015608740864	0.01414984391259105
	13.58472070312499968	0.01327929687500000
	13.58551331496785920	0.01248668503213958
	13.58623702422145280	0.01176297577854671
	13.58689959183673600	0.01110040816326531
	13.58750771604938240	0.01049228395061728
	13.58806720233747200	0.00993279766252739
	13.58858310249307648	0.00941689750692521
	13.58905982905982976	0.00894017094017094
	13.58950125000000000	0.00849875000000000
	1 3.58991 076740035584	0.00808923259964307
	13.59029138321995520	0.00770861678004535
	13.59064575446187008	0.00735424553812872
	13.59097623966942208	0.00702376033057851
	13.59128493827160320	0.00671506172839506
	13.59157372400756224	0.00642627599243856
	13.59184427342689024	0.00615572657311000
	13.59209809027777792	0.00590190972222222
	13.59233652644731392	0.00566347355268638
	13.59256080000000000	0.00543920000000000
	13.59277201076508928	0.00522798923490965
	13.59297115384615424	0.00502884615384615
	13.59315913136347392	0.00484086863652545
	13.59333676268861440	0.00466323731138546
	13.59350479338842880	0.00449520661157025
	13.59366390306122496	0.00433609693877551
	13.59381471221914368	0.00418528778085565
	13.59395778834720512	0.00404221165279429
	13.59409365124964096	0.00390634875035909
	13.59422277777777920	0.00377722222222222
	13.59434560601988608	0.00365439398011287
	13.59446253902185216	0.00353746097814776
	13.59457394809775616	0.00342605190224238
	13.59468017578125056	0.00331982421875000
	13.59478153846153728	0.00321846153846154
	13.59487832874196480	0.00312167125803489
	13.59497081755401984	0.00302918244597906
	13.59505925605536256	0.00294074394463668
	13.59514387733669376	0.00285612266330603
	13.59522489795918336	0.00277510204081633
	13.59530251934140160	0.00269748065859948
	13.59537692901234688	0.00262307098765432
	13.59544830174516736	0.00255169825483205
	13.59551680058436864	0.00248319941563185
	13.59558257777777664	0.00241742222222222
	13.59564577562326784	0.00235422437673130
	13.59570652723899648	0.00229347276100523
	13.59576495726495744	0.00223504273504274
	13.59582118250280448	0.00217881749719596
	13.59587531250000128	0.00212468750000000
	13.59592745008382976	0.00207254991617132
	13.59597769185008896	0.00202230814991077
	13.59602612861082880	0.00197387138917114
	13.59607284580498944	0.00192715419501134
	13.59611792387543296	0.00188207612456747
	13.59616143861546752	0.00183856138453218
	13.59620346148764672	0.00179653851235302
	13.59624405991735552	0.00175594008264463
	13.59628329756343808	0.00171670243656104
	13.59632123456790016	0.00167876543209877
	13.59635792778649856	0.00164207221350078
	13.59639343100189184	0.00160656899810964
	13.59642779512082176	0.00157220487917678
	13.59646106835672320	0.00153893164327750
	13.59649329639889152	0.00150670360110803
	13.59652452256944384	0.00147547743055556
	13.59655478796896512	0.00144521203103412
	13.59658413161182976	0.00141586838817160
	13.59661259055198464	0.00138740944801551
	13.59664020000000000	0.00135980000000000
	13.59666699343201536	0.00133300656798353
	13.59669300269127424	0.00130699730872741
	13.59671825808275968	0.00128174191724008
	13.59674278846153984	0.00125721153846154
	13.59676662131519232	0.00123337868480726
	13.59678978284086784	0.00121021715913136
	13.59681229801729536	0.00118770198270591
	13.59683419067215360	0.00116580932784636
	13.59685548354515456	0.00114451645484387
	13.59687619834710784	0.00112380165289256
	13.59689635581527552	0.00110364418472527
	13.59691597576530688	0.00108402423469388
	13.59693507713994752	0.00106492286005169
	13.59695367805478656	0.00104632194521391
	13.59697179584121088	0.00102820415879017
	13.59698944708680192	0.00101055291319857
	13.59700664767331328	0.00099335232668566
	13.59702341281241088	0.00097658718758977
	13.59703975707930368	0.00096024292069769
	13.59705569444444416	0.00094430555555556
	13.59707123830339328	0.00092876169660542
	13.59708640150497280	0.00091359849502822
	13.59710119637781760	0.0008988036221 8256
	13.59711563475546368	0.00088436524453694
	13.59712972800000000	0.00087027200000000
	13.59714348702444032	0.00085651297556059
	13.59715692231384576	0.00084307768615537
	13.59717004394531328	0.00082995605468750
	13.59718286160687360	0.00081713839312541
	13.59719538461538304	0.00080461538461538
	13.59720762193345280	0.00079237806654624
	13.59721958218549248	0.00078041781450872
	13.59723127367290368	0.00076872632709594
	13.59724270438850560	0.00075729561149476
	13.59725388203017984 ё	0.00074611796982167
	13.59726481401383936	0.00073518598615917
	13.59727550748574720	0.00072449251425222
	13.597285969334172161 0.00071403066582651
	13.59729620620050688	0.00070379379949278
	13.59730622448979456	0.00069377551020408
	13.59731603038076672	0.00068396961923444
	13.59732562983534848	0.00067437016464987
	13.59733502860775424	0.00066497139224412
	13.59734423225308672	0.00065576774691358
	13.59735324613555200	0.00064675386444709
	13.59736207543629312	0.00063792456370801
	13.59737072516081408	0.00062927483918738
	13.59737920014609152	0.00062079985390796
	13.59738750506733824	0.00061249493266069
	13.59739564444444416	0.00060435555555556

Итак, какой же фактор определяет предельный энергетический уровень электрона атома водорода? Чтобы ответить на этот вопрос, обратим внимание на реликтовый диапазон (табл. 11, 12, 13). Это максимум интенсивности излучения Вселенной. Длина волны этого излучения около миллиметра. Возникает вопрос: не является ли реликтовый диапазон верхним пределом существования самых больших фотонов?

Нижний предел радиуса фотона, соответствующий гамма фотону (табл. 11, 12, 13), не вызывает сомнений. Чтобы найти верхний предел радиуса фотона, надо найти последний энергетический уровень электрона атома водорода. Далее из энергии фотона, соответствующего этому уровню, вычесть энергию фотона, соответствующую предпоследнему энергетическому уровню. Если полученная разность энергий будет соответствовать энергии фотона реликтового диапазона, то это будет веским доказательством того, что этот диапазон является верхним пределом для единичных фотонов. В табл. 12 фотон, соответствующий максимуму реликтового излучения, имеет энергию 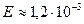eV.

Определим более точное значение энергии фотона, длина волны которого равна длине волны максимума (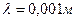) реликтового излучения (рис. 7).

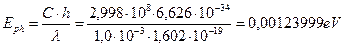(61)

Как видно (табл. 14), эта энергия близка к энергии связи (0,00123337 eV) электрона атома водорода в момент пребывания его на 105 энергетическом уровне. Физический смысл этой энергии заключается в том, что она равна энергии фотона, который должен излучить электрон, вступая в связь с протоном из свободного состояния. Величину энергии этого фотона, соответствующую энергии связи электрона с протоном в момент формирования атома водорода, можно получить двумя способами.

Первый: вычесть из энергии ионизации (13,59800000 eV) атома водорода энергию возбуждения, соответствующую 105 энергетическому уровню (табл. 14) (13,5967662eV).

13, 598000000 eV-13,5967662 eV =0,0012338eV (62)

Второй: по формуле (32), определяющей закон изменения энергии связи электрона с ядром атома

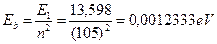(63)

Итак, мы получили результат, следующий из экспериментальной спектроскопии и подтверждающий нашу гипотезу: реликтовый диапазон – верхний предел существования больших фотонов.

Полученное доказательство усилится, если найдем величину энергии фотона, соответствующую не максимуму интенсивности реликтового диапазона, а максимальной длине волны 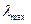этого излучения (рис. 7). Для этого вычтем из энергии возбуждения 105 энергетического уровня энергию возбуждения, соответствующую 104 энергетическому уровню (табл. 14). В результате будем иметь

13,596766621 -13,596742788 = 0,000024 eV. (64)

Эта энергия соответствует примерно максимально возможной длине волны фотона

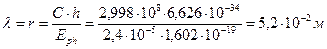. (65)

На рис. 7,b эта длина справа от максимума реликтового излучения, то есть соответствует не максимуму интенсивности реликтового диапазона, а максимальной длине волны 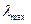этого излучения. Если начало реликтового диапазона электромагнитного излучения соответствует максимально возможной длине волны фотона, равной 0,05 м, то электрон атома водорода излучит такой фотон при переходе со 105 на 104 энергетический уровень (табл. 14).

Далее, если электрон будет излучать фотоны при каждом последовательном переходе, начиная со 105, то длины волн таких фотонов будут увеличиваться ступенчато, оставаясь меньше длины волны максимума реликтового излучения 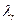= 0,0012338eV, вплоть до 28 энергетического уровня.

Энергия фотона, излученного электроном при переходе с 28 на 27 энергетический уровень, будет равна

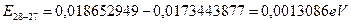. (66)

При последующих последовательных переходах на более низкие энергетические уровни, энергии излученных фотонов будут увеличиваться и переходить из зоны реликтового диапазона в зону инфракрасного излучения (табл. 14 и рис. 7).

Дальше мы увидим, что в невозбужденных атомах и молекулах электроны находятся на нижних энергетических уровнях (2, 3, 4, 5..) и если они переходят с верхних энергетических уровней на нижние, не пропуская ни одной ступени, то появляется ещё одна гипотеза природы Реликтового излучения. Оно формируется рождающимися атомами химических элементов. Тогда существование максимума Реликтового излучения – свидетельство молодости Вселенной.

Да, не просто разгадывать тайны Мироздания. Теперь уже три гипотезы претендуют на разгадку тайны Реликтового излучения. Гипотеза остывающей Вселенной после Большого взрыва и наши две гипотезы: гипотеза устаревших фотонов и гипотеза молодости Вселенной. Какая из них ближе к реальности? Вопрос непростой, однако, объём экспериментальной информации, накопленной к этому моменту, позволяет надеяться на скорое получение окончательного ответа на него.

Таким образом, максимальная длина волны единичных фотонов соответствует Реликтовому диапазону, а минимальная - гамма диапазону (табл. 11, 12, 13, 14). От реликтового диапазона до гамма диапазона длина волны фотона уменьшается на 15 порядков, а частота увеличивается настолько же. Так как фотоны всех диапазонов движутся с одной и той - же скоростью 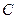и так как они же формируют и волны, ошибочно названного электромагнитного излучения (рис. 8), то скорость (назовем это излучение правильно) фотонного излучения всех диапазонов одна и та же.

Итак, предлагаемая гипотеза делит шкалу излучений на два класса: фотонный и волновой. Фотоны - единичные электромагнитные образования, излучаются электронами атомов. Совокупность фотонов, излученных электронами атомов, формирует поле, которое ошибочно названо электромагнитным. Оно может быть непрерывным или импульсным – волновым (рис. 8).

Если наши суждения верны, то из анализа движения полученной модели фотона мы должны вывести аналитически все соотношения (49)-(56), описывающие его поведение. Для этого мы должны проследить за волновым движением центра масс 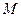всего фотона и центров масс 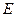отдельных его электромагнитных полей (рис. 10, а).

На рис. 11 показана схема перемещения центра масс 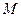фотона и центра масс 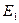одного его электромагнитного поля в интервале длины 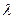одной волны [1], [2].

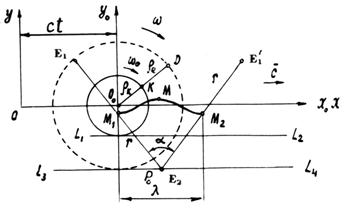
Рис. 11. Схема движения центра масс М фотона и центра масс 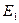одного его электромагнитного поля

Движение центра масс 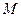фотона моделирует точка 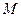, расположенная на расстоянии 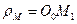от центра условной окружности радиуса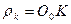или от геометрического центра 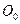фотона.

Движение центра масс 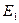одного электромагнитного поля фотона моделирует точка 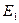, расположенная на расстоянии от центра масс 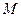фотона [1], [2].

Дата добавления: 2014-01-04