Линейная алгебра. Основная часть команд для решения задач линейной алгебры содержится в библиотеках linalg и LinearAlgebra

Основная часть команд для решения задач линейной алгебры содержится в библиотеках linalg и LinearAlgebra. Поэтому перед решением задач с матрицами и векторами следует загрузить эту библиотеку командой with(linalg) и/или with(LinearAlgebra).

Для определения матрицы в Maple можно использовать команду
matrix(n, m, [[a₁₁,a₁₂,…,a_1n], [a₂₁,a₂₂,…,a_2m],…, [a_n1,a_n2,…,a_nm]]), где n - число строк, m – число столбцов в матрице. Эти числа задавать необязательно, а достаточно перечислить элементы матрицы построчно в квадратных скобках через запятую. Например:

>A:=matrix([[1,2,3],[-3,-2,-1]]);

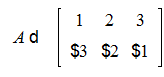
В Maple матрицы специального вида можно генерировать с помощью дополнительных команд. В частности диагональную матрицу можно получить командой diag. Например:

>J:=diag(1,2,3);

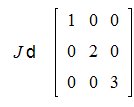
Единичную матрицу можно получить используя ключевое слово identity:
>E:=Matrix(4,4,shape=identity);

или
>E:=array(identity,1..4,1..4):

>E:=evalm(E);

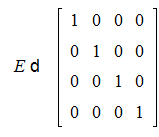
Число строк в матрице А можно определить с помощью команды rowdim(A), а число столбцов – с помощью команды coldim(A).

>rowdim(A);

2

>coldim(3);

3

Сложение двух матриц одинаковой размерности осуществляется теми же командами, что и сложение векторов: evalm(A+B) или matadd(A,B).

>A:=matrix([[1,0],[0,-1]]);

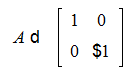
>B:=matrix([[-5,1],[7,4]]);

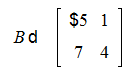
>evalm(A+B):

>matadd(A,B);

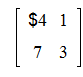
Произведение двух матриц может быть найдено с помощью двух команд:
evalm(A&*B);
multiply(A,B).

В качестве второго аргумента в командах, вычисляющих произведение, можно указывать вектор, например:

>A:=matrix([[1,0],[0,-1]]):

>B:=matrix([[-5,1],[7,4]]):

>v:=vector([2,4]);

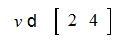
>multiply(A,v):

>evalm(A&*v);

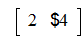
>multiply(A,B):

>evalm(A&*B);

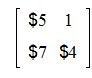
Команда evalm позволяет также прибавлять к матрице число и умножать матрицу на число. Например:

>C:=matrix([[1,1],[2,3]]);

>evalm(2+3*C);

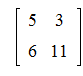
Создадим квадратную матрицу:

>A:=matrix([[4,0,5],[0,1,-6],[3,0,4]]);

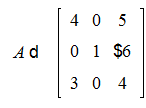
Определитель матрицы А вычисляется командой det(A).
>det(A);

1

Команда minor(A,i,j) возвращает матрицу, полученную из исходной матрицы А вычеркиванием i-ой строки и j-ого столбца.

>minor(A,3,2);

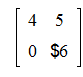
След матрицы А, равный сумме ее диагональных элементов, вычисляется командой trace(A).

>trace(A);

9

Обратную матрицу А^-1, такую что А^-1А=АА^-1=Е, где Е - единичная матрица, можно вычислить двумя способами: evalm(1/A) или inverse(A).

>evalm(1/A):

>inverse(A);

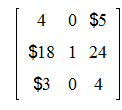
Проверка. Должна получиться единичная матрица.

>multiply(A,%);

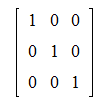
Транспонирование матрицы А – это замена местами строк и столбцов. Полученная в результате этого матрица называется транспонированной и обозначается А'. Транспонированную матрицу А' можно вычислить командой transpose(A).

>transpose(A);

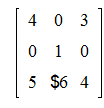
Дата добавления: 2014-01-05