Плоскость в пространстве

Определение. Уравнение вида

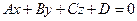(75)

Называется общим уравнением плоскости в системе координат 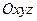. Вектор перпендикулярен плоскости (75); он называется нормальным вектором этой плоскости. Если известно, что плоскость проходит через некоторую точку , то такая плоскость может быть задана уравнением

(76)

Пример. Составить уравнение плоскости с перпендикулярным вектором , проходящей через точку .

Решение. Согласно формуле (76) имеем:

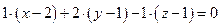, или

Рассмотрим вопрос о взаимном расположении плоскостей в пространстве. Пусть две плоскости заданы уравнениями

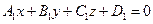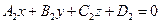и (77)

Угол между плоскостями в пространстве. При любом положении двух плоскостей угол между ними равен углу φ между их нормальными векторами и . Следовательно по формуле 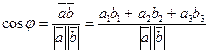, получаем, что угол φ между плоскостями (77) определяется по формуле

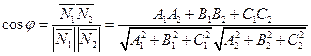(78)

Второй (смежный) угол равен .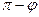

Условие параллельности плоскостей. Если плоскости параллельны, то их нормальные векторы коллинеарны, и наоборот. В этом случае из формулы (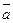и коллинеарны в том и только в том случае, если их координаты пропорциональны:

) получаем условие параллельности плоскостей, заданных уравнениями (77):

(7)

Условие перпендикулярности плоскостей. Если плоскости (77) перпендикулярны, то перпендикулярны между собой и их нормальные векторы. Так как , из формулы (78) получаем условие перпендикулярности двух плоскостей:

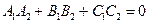(79)

Расстояние от точки до плоскости. Пусть плоскость задана уравнением (75). Тогда расстояние от точки до этой плоскости определяется по формуле:

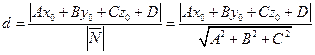(80)

6.2. Прямая в пространстве.

Прямая в пространстве может быть задана как линия пересечения двух плоскостей, т.е. как множество точек, удовлетворяющих системе

(81)

При решении задач чаще используется другой вид уравнений прямой.

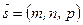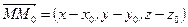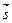Если прямая параллельна вектору , называемому направляющим вектором, и проходит через точку , то ее уравнение может быть получено из условия коллинеарности двух векторов и , где 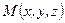произвольная точка прямой. Тогда искомое уравнение прямой будет иметь вид:

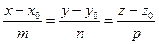(82)

Уравнения (82) называются каноническими уравнениями прямой в пространстве.

Если прямая задана уравнениями общего вида (81), то переход к каноническим уравнениям осуществляется с помощью вычисления координат направляющего вектора 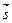из коэффициентов уравнения (81) как соответствующих определителей второго порядка:

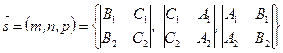(83)

Пример. Найти уравнение прямой, заданной уравнениями общего вида

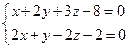
Решение. Сначала определим какую-либо точку 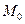, через которую проходит эта прямая. Положим , тогда из данных уравнений получаем систему для определения 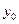и :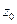

откуда , 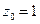. Координаты направляющего вектора находим по формуле (83):

, ,

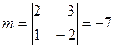По формуле (82) находим каноническое уравнение прямой:

.

Уравнение прямой, проходящей через две данные точк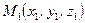и и имеет вид

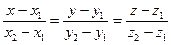(84)

Угол между прямыми. Угол между прямыми в пространстве равен углу j между их направляющими векторам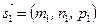и: и 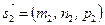, т.е. вычисляется по формуле (78):

(85)

Условие параллельности прямых. Две прямые параллельны тогда и только тогда, когда их направляющие векторы коллинеарны. Поэтому из формулы следует:

(86)

Условие перпендикулярности прямых. Прямые перпендикулярны тогда и только тогда, когда их направляющие векторы перпендикулярны. Из формулы (85) следует искомое условие:

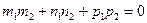(87)

Расстояние от точки до прямой. Пусть дана прямая, проходящая через точку и заданная каноническим уравнением (82), а также точка , находящаяся вне этой прямой. Тогда расстояние 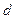от точки 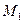до заданной прямой вычисляется по формуле:

(88)

Дата добавления: 2014-01-05