Алгебраические дополнения и миноры

Линейная зависимость и независимость

Определение

Векторы линейного пространства называются линейно независимыми, если их линейная комбинация равна:

(– некоторые числа)

только в одном случае – если:

<здесь – нулевой элемент (но не вектор), а 0 – число>

Векторы – линейно зависимы, если существует такой набор чисел, не все из которых равны нулю, что выполняется равенство:

.

– линейно зависимы

Если – это значит, что диагональ параллелограмма равна нулю, значит стороны равны нулю:

,

.

Но и не равны, т.к. векторы неколлинеарны.

Отсюда следует, что.

Любые три вектора на плоскости линейно зависимы.

Доказать (!)

В пространстве линейно независимыми могут быть не более трех векторов (три некомпланарных вектора линейно независимы).

Любые четыре вектора в пространстве линейно зависимы.

Максимальное число линейно независимых векторов, «помещающихся» в пространстве, – размерность пространства.

Определение

линейно независимых векторов в -мерном пространстве называется базисом этого пространства.

Однако, бывают пространства, не имеющие конечной размерности. Примером такого пространства может служить пространство непрерывных функций. Покажем это. Рассмотрим пространство непрерывных функций на отрезке.

Чтобы показать, что это пространство не является конечномерным, нужно построить бесконечную систему векторов этого пространства, такую, что любое конечное подмножество этой системы векторов было бы линейно независимой системой векторов.

Любое конечное число построенных функций будет линейно независимо. Например:

,

,

. (1)

Равенство верно в любой точке t (!!!)

Равенство верно только когда все.

Тождество (1) выполняется при всех t.

Возьмем точку. В точке:

! Уже равенство (=), а не тождество ()!

Также, подставляя точку, получим, что и т.д.

Т.е. в пространстве (а значит и в) существует любое количество линейно независимых векторов, поэтому такие пространства называются бесконечномерными.

Отметим, что функциональный анализ изучает бесконечномерные пространства и функции в этих пространствах.

Наряду с определителем квадратной матрицы 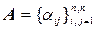рассмотрим определитель

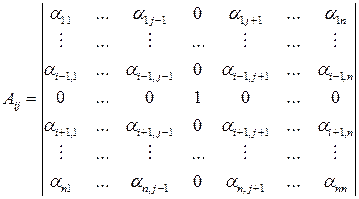, (2.5.1)

называемый алгебраическим дополнением элемента .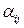

Алгебраическое дополнение элемента 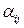по построению не зависит от элементов i- й строки и j -го столбца матрицы A.

Теорема 2.5.1. Определитель матрицы равен сумме произведений элементов какой-либо строки на их алгебраические дополнения, т. е.

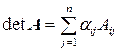. (2.5.2)

Доказательство. В соответствии с ранее установленными свойствами определителей получаем

.

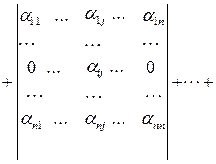
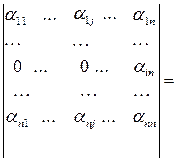
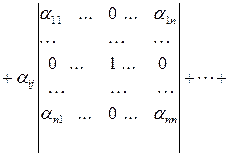
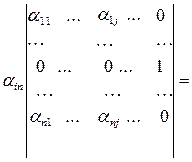
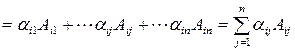Представление определителя матрицы в виде (2.5.2) называется разложением определителя по элементам i-й строки.

Заметим, что в силу равноправности строк и столбцов матрицы справедливо разложение определителя по элементам j -го столбца

.

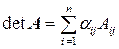Очевидно, что для произвольных чисел 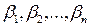в соответствии с формулой (2.5.2) имеем

. (2.5.3)

Теорема 2.5.2. Сумма произведений элементов какой-либо строки на алгебраические дополнения элементов другой строки равна нулю.

Доказательство. Из формулы (2.5.3) следует, что сумма произведений элементов строки 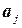на алгебраические дополнения элементов строки равна определителю с двумя одинаковыми строками, равными 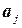. Поэтому

.

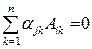Определение 2.5.1. Минором порядка 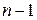называется определитель, который получается из определителя квадратной матрицы после вычеркивания одной строки и одного столбца.

Пусть 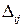— минор, получающийся после вычеркивания i- й строки и
j -го столбца.

Теорема 2.5.3. Справедлива формула .

Доказательство. Для начала рассмотрим алгебраическое дополнение элемента 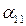, имеем

.

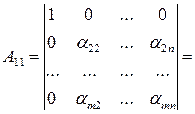
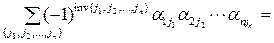
Рассмотрим теперь алгебраическое дополнение (2.5.1). Поменяем последовательно строку с 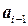, затем с 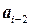и т. д. Проделаем аналогичные операции со столбцами: 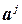меняем местами с , потом с и т. д. Всего местами меняются строк и столбцов. Поэтому ровно 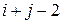раза будет меняться знак определителя, поэтому

.

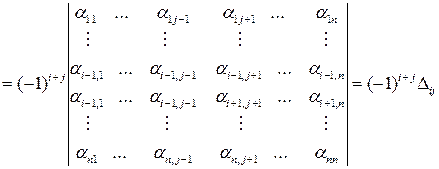Дата добавления: 2014-01-05