Специфіка філософського знання. 11 страница

5. Що таке дисперсія світла? Поясніть її причину.

РОБОТА 5.3

ВИЗНАЧЕННЯ ДОВЖИНИ СВІТЛОВОЇ ХВИЛІ ЗА ДОПОМОГОЮ ДИФРАКЦІЙНОЇ РЕШІТКИ

Мета роботи: вивчити закономірності явищ інтерференції і ди- фракції світла, визначити граничні довжини хвиль видимого світла у

червоній і фіолетовій областях за допомогою дифракційної решітки.

Прилади та обладнання: оптична лава, на якій встановлено джерело світла Л (лампа розжарювання), екран Е з щілиною Щ та дифракційна решітка Д.

Для спостереження дифракційної картини в даній роботі використовують схему, зображену на рис.1.

Е Z Д

Щ

* φ ●

Л

Рис.1

Перед джерелом світла Л (лампою розжарювання) розміщують екран Е, в центрі якого є вертикальна щілина Щ. Дифракційна

решітка встановлюється між екраном та оком спостерігача так, щоб її штрихи були паралельні щілині Щ. Дифракційна картина проек- тується кришталиком на сітчатку ока, куди одночасно проектується і

зображення міліметрової шкали, розміщеної на екрані в площині

щілини. Складається враження, що дифракційний спектр розміщений на поверхні шкали. Але це не так, у площині шкали спектра немає. В цьому легко переконатися, розглянувши її збоку. В площині шкали

розміщено тільки уявне зображення, яке є повною копією ди- фракційного спектра.

Дифракційний спектр складається з центральної білої смуги і розміщених симетрично від неї максимумів першого, другого і більш

високих порядків. Для розрахунків довжини хвилі λ будь-якої лінії у

дифракційному спектрі використовується формула дифракційної

решітки. Вона визначає напрямок головних максимумів у дифрак- ційній картині решітки:

d sin ϕ

= nλ. (1)

З формули решітки (1) випливає, що

d sin ϕ

λ = n

, (2)

де d − період решітки; n − порядок спектра; ϕ − кут дифракції (див. рис.1). При малих його значеннях

sin ϕ

≅ tgϕ =

l

, (3)

z

де l − відстань від центрального максимуму до лінії в уявному спект- рі; z − відстань від решітки до щілини.

Використовуючи останній вираз (3), отримаємо робочу формулу для визначення довжини хвилі:

λ = l ⋅ d n ⋅ z

(4)

Дифракційна решітка – це сукупність великої кількості паралельних, рівновіддалених один від одного штрихів, нанесених на прозору поверхню. Штрихи повністю розсіюють падаюче на них світло і є для нього непрозорими ділянками, а проміжки між штрихами пропускають світло і виконують роль щілин. Штрихи можуть бути нанесені механічним, фото- та голографічним методами тощо. Кількість штрихів N на одиницю довжини визначає можливість застосування дифракційної решітки для роботи в різних

областях спектра. Так, у рентгенівській області

N = 6000, в

ультрафіолетовій − 2000, у видимій − 300, в інфрачервоній – 0,25

штрихів на 1 мм. Відстань d, через яку повторюються штрихи

(рис.2), називається постійною (або періодом) решітки,

d = 1/ N.

Розглянемо проходження світла через дифракційну решітку з періодом d.

1 d 2

φ

∆

φ φ

Рис. 2

Для того, щоб визначити положення максимумів у дифрак- ційній картині, розглянемо дві сусідні щілини (рис. 2) і виберемо в першій щілині будь-яку точку 1. Другу точку 2 виберемо на відстані d від точки 1 (такі точки називають відповідними).

Промені, які виходять з відповідних точок і поширюються під кутом ϕ до напрямку падаючого світла, максимально підсилюють один одного при накладанні, якщо різниця ходу ∆ цих променів

(∆ = d ⋅ sinϕ

) вміщує ціле число довжин хвиль:

d sin ϕ

= nλ

. (5)

Виконання умови (5), наприклад для першої і другої щілин, автоматично означає виконання його для другої і третьої, третьої і четвертої щілин і т. д., тобто для всієї решітки в цілому. Тому формулу (5) називають формулою дифракційної решітки. Ціле число n у формулі (5) називається порядком максимумів, оскільки воно визначає порядковий номер максимуму, відрахованого від

центра екрана (не рахуючи центрального,

n = 0).

Порядок виконання роботи

1. Рисують таблицю.

№     п / п	Задані величини	Результати прямих вимірювань	Результати непрямих вимірювань
d, м	n	z, м	lч, м	lф, м	Червоне світло	Фіолетове світло
< l > < z >	λч, м	< l > < z >	λф, м
с		–				–	–	–	–
						–	–	–	–
< x >			–	–	–
∆ c
ε

2. Визначають постійну решітки за формулою: d =

N, де N −

кількість штрихів, нанесених на 1 мм поверхні решітки (вказана на

корпусі решітки). Наприклад, якщо

N = 100, то d = 0,01мм; при

цьому ∆d

= 5 ⋅10−5 мм і εd

=0,005.

3. Джерело світла, щілину, дифракційну решітку і око розміщують на одній оптичній осі у послідовності, вказаній на рис.1.

4. Розглядають спектри другого порядку. Заносять у таблицю

значення

n = 2, ціни поділок шкал для вимірювання відстані z і l.

5. Визначають графічним методом відношення

l / z

для

червоної границі видимого спектра. Для цього, змінюючи відстань z

від нуля до кількох десятків сантиметрів, використовуючи шкалу

екрана, вимірюють відстань lч

від центра дифракційної картини до

червоного краю спектра другого порядку (лівого чи правого). Червоний край шукають в області, де на нього накладається фіолетова частина спектра третього порядку. Дані записують у таблицю і наносять у вигляді точок на координатній площині, де по осі ординат відкладають значення l, а по осі абсцис – значення z. Графік

залежності l від z повинен бути прямою лінією, яка проходить через

початок координат (z = 0,

l = 0), оскільки величини l і z при

незмінному куті ϕ пропорційні один одному. Лінію проводять так,

щоб відхилення точок від лінії було за можливістю найменшим.

Окремі експериментальні точки не потрапляють на пряму через

похибки вимірювання. Середнє значення відношення

l / z

знаходять,

визначаючи координати крайньої правої точки побудованого графіка.

Значення цих координат позначають через

< l >

та < z >

і вносять у

∆l ∆Z

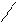таблицю. Величина відносної похибки ε l

Z

= ε l

+ ε Z

= +.

< l > < z >

Вона є мінімальною, тому що для крайньої правої точки графіка максимальне значення l і z.

6. Підраховують довжину хвиль λч

червоної границі видимого

< l >

світла, підставляючи у формулу (4) замість

l / z

значення

< z >,

при цьому всі величини приводять до системи СІ. Кінцевий резуль-

−9

тат виражають у нанометрах, враховуючи, що 1нм=10 м.

7. Визначають похибки вимірювань:

ε = ε + ε

= ε + ∆l

+ ∆ z;

λ d l

z

d < l >

< z >

∆λ=< λ > ⋅ε λ.

8. Повторюють вимірювання і розрахунки п.п. 5−7 для фіолетової границі видимого спектра.

9. Порівнюють отримані в експерименті значення довжини хвиль червоної і фіолетової границі видимого спектра з табличними.

Запитання для самоконтролю

1. Які хвилі називаються когерентними? Які способи отримання когерентних джерел світла вам відомі?

2. Яку відстань називають геометричною різницею ходу? Що називається фазою хвиль? Запишіть зв’язок між різницею фаз і різницею ходу хвиль.

3. У чому полягає явище інтерференції хвиль? Сформулюйте умови максимумів і мінімумів при інтерференції.

4. У чому полягає явище дифракції? Як воно пов’язане з явищем

інтерференції?

5. Сформулюйте принцип Гюйгенса – Френеля і поясніть за його допомогою дифракційну картину, отриману від решітки.

6. Як побудована дифракційна решітка? Що називають постій- ною решітки? Виведіть формулу решітки.

7. Чим відрізняється дифракційний спектр від дисперсійного?

8. Де використовуються дифракційні решітки?

РОБОТА 5.4

ВИЗНАЧЕННЯ КОНЦЕНТРАЦІЇ ОПТИЧНО АКТИВНИХ РЕЧОВИН ПОЛЯРИМЕТРОМ

Мета роботи: вивчити явище повертання площини коливань і принцип роботи поляриметрів, навчитися визначати концентрації оптично активних речовин.

Прилади і матеріали: поляриметр і кювети − трубки з дослі-

джуваними розчинами.

Повертання площини коливань

Деякі кристали (наприклад, кварц), розчини багатьох органічних речовин (наприклад, цукру), а також деякі чисті рідини мають власти- вість повертати площину коливань поляризованого світла навколо осі світлового пучка (рис.1). Такі речовини називають оптично активни- ми. При повертанні площини коливань за годинниковою стрілкою (якщо дивитися назустріч променю) речовину називають правоповер- таючою, при повертанні проти годинникової стрілки – лівоповертаю-

чою. На досліді встановлено, що кут ϕ повороту площини коливань

пропорційний товщині l шару оптично активної речовини, а для роз- чинів – також і концентрації C:

ϕ =ϕ0 ⋅l ⋅C

. (1)

Коефіцієнт пропорційності ϕ0

називають питомим повертан-

ням. Він чисельно дорівнює куту повороту площини коливань при проходженні шару речовини одиничної товщини і одиничної концен-

трації. Питоме повертання ϕ0

залежить від довжини світлової хвилі.

Тому при дослідженні повертання площини коливань користуються лише монохроматичним світлом.

Для розчину з невідомою концентрацією Cx

кут повороту пло-

щини коливань

ϕ x і рівність (1) перепишемо так:

ϕx =ϕ0 ⋅l ⋅Cx

. (2)

Поділивши почленно (2) на (1), одержимо формулу для знахо- дження невідомої концентрації Cx:

ϕx

Cx = C

ϕ

. (3)

Будова та принцип роботи поляриметра

Кут повороту площини коливань можна поміряти спеціальним приладом – поляриметром, основними деталями якого є два ніколі – поляризатор П (рис.2) і аналізатор А, а між ними в кюветі К розмі- щують оптично активну речовину. Вимірювання кута ϕ (або ϕ x) по- чинають за відсутності кювети між поляризатором і аналізатором. По-

вертають аналізатор A доти, поки коливання світлового вектора Er не

будуть повністю погашені (“установлення на темноту”). Це станеться

, коли напрямки коливань

N П і

N A світлового вектора при прохо-

дженні через поляризатор і аналізатор стануть взаємно перпендикуля- рними (рис.3). У таких випадках кажуть, що поляризатор і аналізатор перехрещені.

Якщо тепер між перехрещеними ніколями розмістити кювету з оптично активною речовиною, то внаслідок повороту світлового век-

ϕ

тора на деякий кут (нове положення світлового вектора на рис.3 по-

v

ϕ

значено E

) поле зору прояснюється. Цей кут можна визначити, по-

вертаючи аналізатор до повного гасіння світла доти, поки напрямок

N ′A

коливань світлового вектора променів, які проходять через аналі-

E. Кут повороту аналізатора

затор, стане перпендикулярним вектору ϕ

читають на його шкалі. Він дорівнює куту ϕ повороту площини ко-

ливань.

При вимірюванні користуються монохроматичним світлом, яке одержують за допомогою світлофільтра Ф, розміщеного між джере- лом світла I та поляризатором П (рис.2).

Момент повного затемнення точно визначити неможливо. Тому, пам’ятаючи, що очі чутливі до змін яскравості, для точнішого вимі-

рювання кутів використовують поляриметри з напівтіньовим полем зору. Таке поле складається з двох або трьох частин (рис.4). Його мо- жна одержати різними способами. У найпростішому випадку – за до- помогою спеціальної кварцевої пластинки (напівтіньової), яка повер-

тає вектор Er падаючої на неї світлової хвилі на невеликий кут β (в

положення Er′

на рис.4,а). Напівтіньову пластинку M встановлюють

за поляризатором П так, щоб вона закривала половину (рис.4а), або третину (рис.4,б) поля зору. Щоб поля М і П були однаково яскраві, аналізатор А повертають у таке положення, коли він пропускає коли- вання, перпендикулярні бісектрисі кута β. У цьому випадку аналіза-

тор пропускає малі, але однакові компоненти

E′A і

EA (рис.4,а). Якщо

ж напрямки векторів зміняться на кут ϕ (внаслідок проходження сві-

тла через шар оптично активної речовини), то для вирівнювання яск-

равостей полів аналізатор повертають на такий же кут. Його числове значення читають на шкалі аналізатора. Так працюють кругові поля- риметри − в них повертається аналізатор.

У напівтіньових поляриметрах аналізатор нерухомий, а яскраво- сті полів М і П вирівнюють клиновим компенсатором (рис.5). Він складається із двох кварцевих клинів: рухомого лівоповертаючого

клина, що повертає вектор Er проти годинникової стрілки і нерухомо-

го правоповертаючого - контрклина, який повертає вектор Er за го-

динниковою стрілкою. Переміщуючи рухомий клин відносно контрк-

лина, встановлюють таку сумарну товщину двох клинів на рівні опти- чної осі, при якій кут повороту площини коливань ϕ, обумовлений оптично активною речовиною, компенсується кутом повороту ϕ ′,

обумовленим кварцем, при цьому ϕ

= ϕ′.

o

Сахариметри − це поляриметри, якими можна визначити кон- центрацію сахарози в розчині. В них одночасно з рухомим клином пе- реміщується шкала, проградуйована в міжнародних цукрових граду-

сах(S); 100oS

відповідають

34,62o

кутовим. Сахариметрами безпосе-

редньо визначають масову частину сахарози, виражену у відсотках. Для цього результат, прочитаний на шкалі сахариметра, множать на

перевідний коефіцієнт

0,260

і ділять на густину досліджуваного роз-

чину. Концентрацію ж будь-яких інших оптично активних речовин у розчинах визначають за формулою (3).

Практичне застосування явища оптичної активності описане в додатку до цієї роботи.

Порядок виконання роботи

1. Рисують таблицю.

2. Читають опис поляриметра – знайомляться з його будовою і з’ясовують, якого він типу: круговий, напівтіньовий чи сахариметр.

3. Перевіряють, чи встановлено світлофільтр Ф перед джерелом світла I (рис.2).

4. Виймають з поляриметра кюветку K, вмикають джерело світла і, обертаючи окуляр, добиваються чіткої видимості лінії, яка розділяє поле зору на два порівняльні поля.

5. Визначають ціну поділки шкали аналізатора і записують її значення в таблицю.

6. Установлюють шкалу на нуль: повертають гвинт компен- суючого клина (або аналізатора) доти, поки яскравість всього поля зору (поблизу повного затемнення) стане однаковою. Якщо це зроб- лено вірно, то найменший поворот гвинта вправо чи вліво зумовлює неоднакову яскравість поля зору.

N11

Ј

9 E

NA

Pnc.3

1”

Ј

Li’ V V

VE

z

KA 0 0

VE

Piic.4a Pnc.4ф

ICOHIpKJH

A

C9

pfloMrIflKTmH

Ppic.5

1 50

Читають на шкалі значення початкового кута α0

(він може де-

що відрізнятися від нуля); проти нуля ноніуса читають число цілих одиниць, а порядковий номер тієї поділки ноніуса, яка збігається з по- ділкою нижньої (основної) шкали, дає число десятих і сотих часток одиниці.

Якщо нуль ноніуса зсунутий вліво від нуля нижньої шкали, від- лік беруть із знаком мінус, а десяті і соті частки одиниці визначають за лівою частиною ноніуса.

7. Поміщають у поляриметр кювету з розчином цукру відомої концентрації C. Досягнувши однакової яскравості поля зору (двох його частин – порівняльних полів), читають на шкалі відлік α. Запи- сують значення α і C в таблицю.

№ п/п	Задані величини	Результати прямих вимірювань	Непрямі вимірювання
C, %	o α0, S	o	o	ϕ, o S	ϕx, oS	Cx, %
-	c =	c =	c =	-	-	-
	- - -				- - -	- - -	- - -
< x >
∆c, Pc =1	-				-	-	-
o ∆, Po≥ 0,95					-	-	-
∆, P ≥ 0,95
ε

α, S

α x, S

Примітка. Якщо кювета порожня, її промивають дистильова- ною водою і заповнюють розчином так, щоб не було бульбашок пові- тря: кювету наповнюють до утворення поверх неї випуклого меніска, “зрізають” меніск плоскопаралельною пластинкою, закручують криш- ку кювети так, щоб рідина не просочувалась.

8. Повторюють п. 7 з розчином цукру невідомої концентрації

Cx. Відлік позначають α x.

9. Вимірювання п.п. 6−8 повторюють не менше трьох разів, оде- ржані результати заносять у таблицю.

10. Розраховують середні значення результатів прямих і непря- мих вимірювань:

< ϕ >=<α

> − < α0 >;

< ϕx

>=<αx

> − < α0 >;

< Cx

>=< C >⋅<ϕx >.

<ϕ >

11. Визначають довірчі границі при заданих довірчих імовірно- стях і відносні похибки прямих і непрямих вимірювань. При цьому враховують, що:

C

;

C

ε = ε + ε + ε

x ϕ ϕ x

∆ = ∆ + ∆

;

ϕ α α o

∆ = ∆ + ∆

.

ϕx αx αo

12. Порівнюють одержану точність вимірювань з можливостями методу.

Запитання для самоконтролю

1. Дати визначення плоскополяризованої хвилі, площини коливань, площини поляризації.

2. У чому суть явища поляризації хвиль? Яка специфіка спосте- реження поляризації світла?

3. Записати, сформулювати і пояснити закон Малюса.

4. Пояснити природу подвійного променезаломлення світла, на- звати властивості звичайного і незвичайного променів.

5. Пояснити, чому природне світло неполяризоване і описати спо- сіб одержання поляризованого світла за допомогою призми Ніколя.

6. Описати явище повертання площини коливань.

7. Описати будову і пояснити принцип роботи поляриметра.

Додаток до роботи 5.4

Визначення концентрації оптично активних речовин за допомо- гою поляриметра широко застосовується в цукровій промисловості для технологічного контролю на різних стадіях виробничого процесу: у фармацевтичній промисловості − для реєстрації наявності таких речовин як камфора, кокаїн, нікотин та інших; у медичних та біохімічних лабораторіях − для визначення вмісту цукру та білка в мочі, а також глюкози та цукрози в розчинах; для титрування; для контролю хроматографічного розділення оптично активних речовин; для дослідження кінетики біохімічних реакцій (наприклад, ензимного розщеплення).

Висока чутливість методу дає змогу досліджувати дуже малі маси оптично активних речовин: так в 1 мл розчину можна виявляти

−9

навіть такий вміст глюкози, який не перевищує

2,5 ⋅10

г. Простота

методу робить його високопродуктивним сто і більше проб за годину.

Оптична активність проявляється в речовинах, молекули яких не мають центра або площини симетрії. На основі цього Л. Пастер понад сто років тому започаткував основи стереохімії – вчення про будову молекул. У наш час оптична активність та її дисперсія (залеж- ність від довжини хвилі) ефективно використовується при дослід- женні структури і властивостей біополімерів – білків та нуклеїнових кислот. Вони, як правило, мають спіральну структуру і високу оптичну активність, яка не є однаковою вздовж і поперек спіралі. Речовини з несиметричними молекулами – синтетичні і ті, що зустрічаються в неживій природі, мають однакові кількості молекул з лівою та правою асиметрією. І тому в своєму загальному об’ємі не проявляють оптичної активності, на відміну від найважливіших речовин живої природи – білків, ліпідів, вуглеводів, нуклеїнових кислот, амінокислот, які існують лише у вигляді чисто асиметричних форм, антиподів.

При цьому антиподи однієї асиметрії (наприклад, лівої) не можуть замінятися антиподами іншої асиметрії (правої). Наприклад, із розчину синтетичного цукру бактерії, які ним живляться, засвоюють

лише правоповертаючі молекули. Коли весь правоповертаючий цукор з’їдено, бактерії починають голодувати, хоч і знаходяться у розчині лівоповертаючого цукру.

Той факт, що асиметрія оптичної активності характерна лише для живих організмів і речовин органічного походження, дає змогу вирішувати різноманітні наукові проблеми. Наприклад, виявлення оптичної активності нафти стало переконливим свідченням її орга-

нічного походження. А відсутність оптичної активності в аміно- кислот, знайдених у 1970 році в складі метеорита, доказало їхнє неземне походження. Причини біологічної доцільності асиметрії в речовинах живої природи до цього часу остаточно не встановлені.

РОБОТА 5.5

ВИВЧЕНННЯ ОПТИЧНОГО КВАНТОВОГО ГЕНЕРАТОРА

Мета роботи: вивчити принцип дії квантового генератора на при- кладі гелій-неонового лазера і дослідити монохроматичність, когерент- ність, направленість та поляризацію лазерного випромінювання.

Прилади та обладнання: оптична лава, на якій встановлено ге-

лій-неоновий лазер ЛГН-105, поляроїд, екран із щілиною, дифракцій- на решітка, екран з двома щілинами, суцільний екран (аркуш білого паперу), лінійка.

Оптичним квантовим генератором (лазером) називають прилад, в якому здійснюється генерація монохроматичних електромагнітних хвиль оптичного діапазону в результаті вимушеного (індукованого) випромінювання.

Активним елементом гелій-неонового лазера є газорозрядна

Дата добавления: 2014-01-05