Rocket propulsion

We now consider specifically how the speed of the rocket varies as the burnt fuel is expelled. When dealing with rockets we are usually given the velocity of the exhaust gases relative to the rocket; that is, v _ex = v _GR. If the rocket is moving at velocity v _RE relative to the earth, then the velocity of the gases relative to the earth is v_GE = v_GR +v_RE.

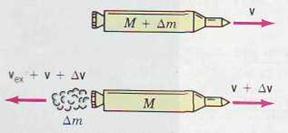
Consider a rocket of mass M with fuel of mass ∆ m. Their common velocity is v relative to some inertial frame; see Fig. 5.6 a. When the rocket engines are fired, the gases are expelled backward with an exhaust velocity v _ex = υ_ex i relative to the rocket. This is a fixed quantity determined by the design of the engine and the type of fuel. If the rocket's velocity changes to v + ∆ v relative to the inertial frame, the velocity of the exhaust gas relative to this frame will be v _gas = v _ex + v + ∆ v = (υ_ex + υ + ∆ υ) i, as shown in Fig. 5.6 b. The component form of the law of conservation of momentum becomes

∑ p_x: (M + ∆m) υ = M (υ + ∆ υ) + ∆m (−υ_ex + υ + ∆ υ)

After some cancellation we find

0 = M ∆ υ + ∆m (−υ_ex + ∆ υ)

If both ∆ υ and ∆m are small quantites relative to υ and M, respectively, their product, ∆υ∆m, is negligible in comparison with the other terms, and we are left with

FIGURE 5.6 (a) A rocket of mass M with fuel ∆m moving at velocity v relative to an inertial frame. (b) After the fuel is expelled at velocity v_ex relative to the rocket, the velocity of the rocket is v+∆v relative to the inertial frame.

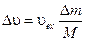(i)

To proceed further, we must reduce the number of variables. Since an increase in the mass of the expelled gases corresponds exactly to the loss in mass of the rocket system, we have ∆m = −∆M. In the limit as ∆ M →0, (i) becomes d υ = − υ _exdM/M. On integrating both sides

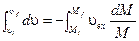
we find

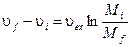(5.17)

We see that the change in the velocity of the rocket is directly proportional to the exhaust speed. Since the change in velocity depends on the ratio of M _i = mass of rocket + fuel to M _f = mass of rocket alone, the mass of the fuel should be as large as possible. Through the use of multiple stages the mass of the rocket is reduced as each empty fuel tank is discarded. When the fuel is expelled as a continuous stream, as it is here, the final velocity is independent of the rate at which mass is expelled.

It is interesting to note that a rocket gains more kinetic energy from a given quantity of fuel when the rocket is traveling at high speed than when it is moving at low speed. The combus­tion of the fuel releases a certain amount of energy that is shared between the rocket and the exhaust gases. When the rocket is moving slowly, the gases travel at a speed close to υ_ex relative to an inertial frame and take a large fraction of the energy available. When the rocket is traveling at high speed, the gases move at lower speed relative to the inertial frame, and the rocket gains a larger fraction of the energy. When the speed of the rocket reaches υ_ex, the expelled gases are brought to rest relative to the inertial frame. At this point, the rocket takes all the energy.

CHAPTER 6

Rotation of a Rigid Body about a Fixed Axis

Дата добавления: 2014-01-05