Постановка задачи. Точечные оценки неизвестных параметров распределения

Материал основной части лекции.

ПЛАН

Л Е К Ц И Я

по дисциплине «Теория вероятностей и математическая статистика» для бакалавров направления 080100.62 «Экономика»

Тема № 3. Основы математической статистики.

Занятие № 3.3Статистическая оценка неизвестных параметров распределения.

Вид занятия: лекция (16)

Литература: 1). Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб.пособие для вузов.-8-е изд.,стер.-М.:Высш.шк.,2012-479 с. (197-201,205-207,213). 2.) Вентцель Е.С. Теория вероятностей. Учебник М.: ACADEMIA, 2003-572с .(127-155). 3) Теория вероятностей и математическая статистика для экономистов: Уч.пособие/А.М. Карлов. – М.: КНОРУС, 2011. -264 с. (203 -242) 4 .) А.И.Герасимович, Я.И.Матвеева Математическая статистика. Мн. «Вышэщ.школа», 1978-200 с. (25-52).

проведения занятия

№ п/п	Учебные вопросы занятия	Время, мин.
I. II	Вводная часть: Объявление темы, темы занятия. Постановка учебных целей занятия. Основная часть.	2-3
	1.Постановка задачи. Точечные оценки неизвестных параметров распределения. 2.Генеральное и выборочное среднее арифметическое значение. 3.Генеральная и выборочная дисперсии. 4.Интервальные оценки неизвестных параметров распределения. Доверительная вероятность и доверительный интервал.
	Заключительная часть	2-3
	Подведение итогов занятия. Выдача задания на самостоятельную работу.

Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретичес­ких соображений удалось установить, какое именно рас­пределение имеет признак. Естественно возникает задача оценки параметров 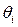, которыми определяется это распреде­ление.

Например, если известно, что изучаемый признак 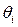распределен в генеральной совокупностинормаль­но,то необходимо оценить (приближенно найти) матема­тическое ожидание 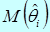исреднее квадратическое отклонение 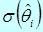, так как эти два параметра полностью определяют нормаль­ное распределение.Если же есть основания считать, чтопризнак 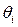, имеет, например, распределение Пуассона, то необходимо оценить параметр λ, которым это распреде­ление определяется.

Обычно в распоряжении исследователя имеются лишь данные выборки, например, значения количественного признака 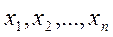,полученные в результате «n» наблюдений(здесь и далее предполагаем, что наблюдения являются независимыми).Именно через данные выборки и находят (выражают) оцениваемый параметр.

Рассматривая 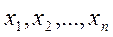как независимые случайные величины 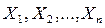,можно сказать, чтонайти статистическую оценку неизвестного параметра теоретиче­ского распределения — это значит найти функцию от наблюдаемых случайных величин, которая и дает при­ближенное значение оцениваемого параметра.

Например, как будет показано далее, для оценки математического ожидания нормального распределенияслужит функция (среднее арифметическое наблюдаемых значений признака) .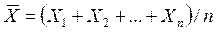

Итак, статистической оценкой неизвестного пара­метра теоретического распределения называют функцию от наблюдаемых случайных величин.

Статистические оценки неизвестного параметра подразделяются на: точечные оценки и интервальные оценки.

Точечной оценкой неизвестного параметра называют статистическую оценку, определяемуюодним числом .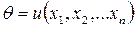

Интервальной оценкой неизвестного параметра называют статистическую оценку, определяемую двумя числами и 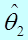- концами интервала, накрывающего оцениваемый параметр.

Точечные оценки неизвестного параметра распределения

Из вышеприведенного материала следует, чтоточечной оценкой неизвестного параметра 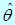является функция 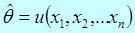, зависящая от наблюденных значений случайной величины,которая может быть использована для нахождения приближенного значения неизвестного параметра . Таким образом, нас интересуют только определенны классы функций, близкие в определенном смысле к оцениваемому параметру 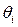. Имеется специальный раздел математической статистики — теория оценивания, который занимается выработкой правил конструирования функций 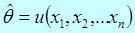для нахождения точечных оценок неизвестных параметров.

Сформулируемосновные свойства, которые должны иметь «хорошие» оценки неизвестного параметра .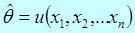

Прежде всего,с точки зрения точности и надежности оценок, желательно, чтобынайденные,на основании выбо­рочных функций, 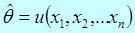оценки неизвестных параметров по возможности были тесно сконцентрирова­ны около значений оцениваемых параметров, другими словами, чтобырассеивание случайной величины 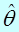около было по возможности наименьшим.

Определение 1.

Оценка 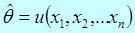называется состоятельной, если при увеличении числа измерений оценка стремится (сходится) по вероятности к оцениваемому пара­метру, т. е. если

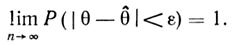(1.1)

Требование состоятельностигарантирует от грубых оши­бок 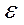в определении при достаточно больших «п».

Определение 2.

Оценка 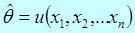называется несмещенной (оценкой без систематической ошибки), если ее математическое ожидание равно оцениваемому па­раметру, т. е. если

(1.2)

Если условие (1.2) не выполняется, тооценка называ­ется смещенной(содержащей систематическую ошибку).

Таким образом смещённой называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Часто наряду с несмещенными оценками 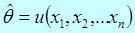применяются асимптотически несмещённые оценки,т.е. такие оценки, для которыхпри увеличении объёма выборки.

Следует заметить, чтов теории ошибок измеренийсистематическими ошибкаминазы­ваютнеслучайные ошибки, искажающие результаты измерений в одну определенную сторону(в одном направлении – в направлении увеличения или уменьшения результата измерений).Например,измерение длины растянутой рулет­кой, измеряющей расстояния, систематически дает заниженные результаты.

Состоятельные, несмещенные или асимптотически не­смещенные оценки могут быть получены различными ме­тодами.Например,две оценки математического ожида­ния – среднее арифметическое 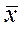ивыборочная медиана - являются несмещёнными и состоятельными оценками. Графическое распределение этих оценок, представленное на Ри.1.1,позволяет сделать вывод о том, чтоиз этих двух оценок целесообразнее выбрать 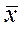,так как очевидно, чтодисперсия этой оценки меньше, дисперсия выборочной медианы .

Рис.1.1. Распределения выборки по среднему арифметическому значению и по значению медианы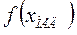

В строгих курсах математической статистики доказывается, чтодисперсия любой несмещённой оценки одного параметра удовлетворяет неравенству Рао – Крамера:

(1.3)

где f(x,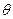) — плотность распределения вероятностей слу­чайной величины; N — число произведенных испытаний. Следует заметить, что оценка параметра может быть получена по каждому из N испытаний.

Определение 3. Оценка 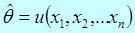, для кото­рой в неравенстве Рао — Крамера (1.3) достигается знак равенства, называетсяэффективной.

Иначе можно сказать – эффективной оценкой называют статистическую оценку, которая (при заданном объеме выборки «п») имеет наименьшую воз­можную дисперсию.

При рассмотрении выборок большого объема (п вели­ко!)к статистическим оценкам предъявляется требование состоятельности (см. определение 1).

Определение 4. Оценка 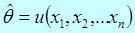называет­ся достаточной, если она использует всю информацию от­носительно оцениваемого параметра, содержащуюся в выборке.

Достаточные оценки построены таким образом, что никакие другие оценки не могут дать какой-либо дополнительной информации об оцениваемых параметрах.

Кроме указанных свойств, которые должны иметь «хорошие» оценки неизвестного параметра 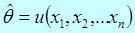, имеются и другие свойства, которые должны иметь хорошие оценки. Например,желательно, чтобы оценки параметров имели линейный вид. Следует заметить, что, к сожалению, далеко не всегда возможно найти такие функции 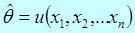, которые имели бы все указанные свойства.

Дата добавления: 2014-01-05