Групповая и общая средние

Допустим, чтовсе значения количественного при­знака X совокупности, безразлично - генеральной или вы­борочной, разбиты на несколько групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти ее среднюю арифметическую.

Групповой среднейназываютсреднее арифметическое значений признака, принадлежащих группе.

Общей средней 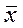называютсреднее арифметическое значений признака, принадлежащих всей совокупности.

Зная групповые средние и объемы групп, можно найти общую среднюю: общая средняяравна средней арифмети­ческой групповых средних, взвешенной по объемам групп.

Опуская доказательство, приведем иллюстрирующий пример.

Пример. Найти общую среднюю совокупности, состоящей из сле­дующих двух групп:

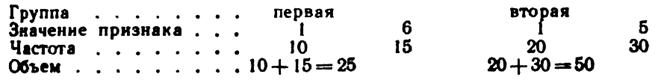Решение.

Найдём групповые средние:

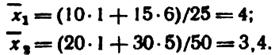Найдем общую среднюю по групповым средним:

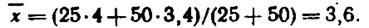Замечание 1.Для упрощения расчета общей средней совокуп­ности большого объемацелесообразно разбить ее на несколько групп, найти групповые средние и по ним общую среднюю.

Замечание 2.

На практикечасто бывает необходимым использоватьпонятие отклонения от общей среднейиего 2 свойства.

Отклонением называют разность 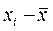между значением признака 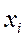и общей средней .

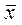Свойство №1.

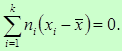Сумма произведений отклонений на соответствующие частоты равна нулю:

(2.10)

Доказательство данного свойства приведём на примере.

Пример. Дано следующее распределение количественного признака X:

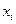
ni

Убедиться, что сумма отклонений на соответствующие частоты равна нулю.

Решение.

Найдём общую среднюю:

Найдём сумму произведений отклонений на соответствующие частоты:

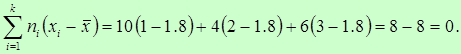Что и требовалось доказать.

Свойство №2.

Среднее значение отклонения равно нулю.

Действительно, с учётом свойства №1 отклонения, получим:

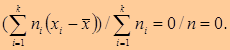(2.11)

Дата добавления: 2014-01-05