Пример 3.1. Рассмотрим алгебру , , , где множество действительных чисел,

Рассмотрим алгебру 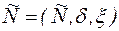, , 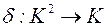, 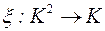где 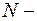множество действительных чисел, 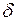представляет собой операцию сложения, а 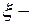операцию умножения. Таким образом, нами рассматривается кольцо 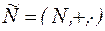. Необходимо проверить, является ли алгебра 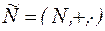кольцом?

Решение

1. Проверим алгебру относительно операции сложения.

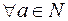- , выполняется свойство коммутативности ;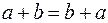

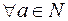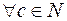- , , выполняется свойство ассоциативности

;

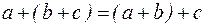- в множестве 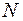есть число «0» (ноль), для которого справедливо

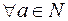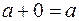, ; по определению число «0» является единицей кольца относительно операции сложения;

- в множестве 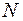для любого числа 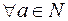найдётся обратный ему элемент , .

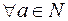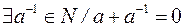- операция сложения коммутативна ;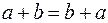

2. Проверим алгебру относительно операции умножения.

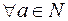- , свойство коммутативности выполняется ;

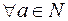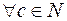- , , выполняется свойство ассоциативности

;

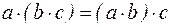- в множестве 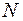есть число «1» (единица), для которого справедливо

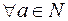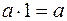, ; по определению число «1» является единицей кольца относительно операции умножения.

- операция умножения коммутативна ;

Таким образом, алгебра 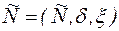представляет собой коммутативное кольцо с единицей.

Вопросы к разделу №3.

1. Дайте определение алгебраической системы. Запишите высказывательную форму.

2. Какие алгебраические системы называются однотипными?

3. Какие алгебраические системы называются конечными?

4. Какие алгебраические системы называются конечного типа?

5. Какое множество называется замкнутым относительно операции?

6. Какое отображение называется морфизмом алгебраических систем?

7. Что называется мономорфизмом? Гомоморфизмом? Изоморфизмом?

8. Дайте определение автоморфизма.

9. Сформулируйте теорему об обратном изоморфизме. Приведите доказательство теоремы.

10. Сформулируйте теорему о композиции изоморфизмов. Приведите её доказательство.

11. Что называется полугруппой?

12. Дайте определение левой и правой единицы полугруппы, а также просто единицы.

13. Что называется моноидом?

14. Дайте определение левого и правого нуля полугруппы, а также просто нуля.

15. Что называется левым и правым обратимым элементом?

16. Дайте определение группы.

17. Какая группа называется абелевой?

18. Что такое морфизм групп?

19. Сформулируйте теорему о переводе морфизмом групп единицы в единицу.

20. Сформулируйте теорему о переводе морфизмом групп нуля в ноль.

21. Сформулируйте теорему о переводе морфизмом групп обратного элемента в обратный элемент.

22. Какая универсальная алгебра называется кольцом?

23. Дайте определение кольца с единицей.

24. Приведите примеры колец.

Дата добавления: 2014-01-05