
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Процентной ставке
|
|
|
|
ДИСКОНТИРОВАНИЕ ПО СЛОЖНОЙ
Оценивая целесообразность финансовых вложений в тот или иной вид бизнеса, исходят из того, являются ли эти вложения более прибыльными (при допустимом уровне риска), чем вложения в государственные ценные бумаги. Используя несложные методы, пытаются проанализировать будущие доходы при минимальном, "безопасном" уровне доходности.
Основная идея этих методов заключается в оценке будущих поступлений 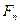 (например, в виде прибыли, процентов, дивидендов) с позиции текущего момента. При этом, сделав финансовые вложения, инвестор обычно руководствуется тремя посылками: а) происходит перманентное обесценение денег (инфляция); б) темп изменения цен на сырье, материалы и основные средства, используемые предприятием, может существенно отличаться от темпа инфляции; в) желательно периодическое начисление (или поступление) дохода, причем в размере не ниже определенного минимума. Базируясь на этих посылках, инвестор должен оценить, какими будут его доходы в будущем, какую максимально возможную сумму допустимо вложить в данное дело исходя из прогнозируемой его рентабельности.
(например, в виде прибыли, процентов, дивидендов) с позиции текущего момента. При этом, сделав финансовые вложения, инвестор обычно руководствуется тремя посылками: а) происходит перманентное обесценение денег (инфляция); б) темп изменения цен на сырье, материалы и основные средства, используемые предприятием, может существенно отличаться от темпа инфляции; в) желательно периодическое начисление (или поступление) дохода, причем в размере не ниже определенного минимума. Базируясь на этих посылках, инвестор должен оценить, какими будут его доходы в будущем, какую максимально возможную сумму допустимо вложить в данное дело исходя из прогнозируемой его рентабельности.
Базовая расчетная формула для такого анализа является следствием формулы (4.3):
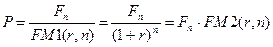 (4.20)
(4.20)
где 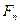 - доход, планируемый к получению через
- доход, планируемый к получению через  лет;
лет;
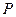 - текущая (или приведенная) стоимость (present value), т.е. оценка величины
- текущая (или приведенная) стоимость (present value), т.е. оценка величины 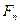 с позиции текущего момента;
с позиции текущего момента;
 - процентная ставка.
- процентная ставка.
Экономический смысл такого представления заключается в следующем: прогнозируемая величина денежных поступлений через  лет
лет  с позиции текущего момента будет меньше и равна
с позиции текущего момента будет меньше и равна 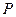 (поскольку знаменатель дроби больше единицы). Это означает также, что для инвестора сумма
(поскольку знаменатель дроби больше единицы). Это означает также, что для инвестора сумма 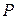 в данный момент времени и сумма
в данный момент времени и сумма 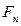 через
через 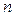 лет одинаковы по своей ценности.
лет одинаковы по своей ценности.
Аналогично случаю простых процентов процесс нахождения 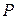 по
по 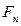 по формуле (4.20) называется математическим дисконтированием, т.е. решается задача нахождения такой величины капитала
по формуле (4.20) называется математическим дисконтированием, т.е. решается задача нахождения такой величины капитала 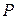 , которая через
, которая через 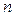 лет при наращении по сложным процентам по ставке
лет при наращении по сложным процентам по ставке  будет равна
будет равна 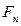 . Как и ранее, разность
. Как и ранее, разность  между
между 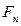 и
и 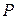 называется дисконтом:
называется дисконтом:
 (4.21)
(4.21)
Множитель  называется дисконтным множителем (discount factor), его значения табулированы. Величина
называется дисконтным множителем (discount factor), его значения табулированы. Величина  представляет собой коэффициент дисконтирования. Экономический смысл дисконтного множителя
представляет собой коэффициент дисконтирования. Экономический смысл дисконтного множителя 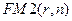 заключается в следующем: он показывает "сегодняшнюю" цену одной денежной единицы будущего, т.е.
заключается в следующем: он показывает "сегодняшнюю" цену одной денежной единицы будущего, т.е.
т.е. чему с позиции текущего момента равна одна денежная единица (например, один рубль), циркулирующая в сфере бизнеса 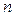 периодов спустя от момента расчета, при заданной процентной ставке (доходности)
периодов спустя от момента расчета, при заданной процентной ставке (доходности)  . По поводу соблюдения строгости при записи множителя
. По поводу соблюдения строгости при записи множителя 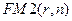 справедливо замечание, аналогичное сделанному в связи с множителем
справедливо замечание, аналогичное сделанному в связи с множителем 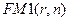 .
.
Очевидно, что значение дисконтного множителя убывает с ростом 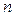 . Увеличение процентной ставки
. Увеличение процентной ставки  также уменьшает величину дисконтного множителя. Следовательно, при такого рода изменениях
также уменьшает величину дисконтного множителя. Следовательно, при такого рода изменениях 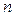 и
и  приведенная стоимость уменьшается.
приведенная стоимость уменьшается.
По формуле (4.20) происходит учет (математический) капитала из сложных процентов "на 100". Поясним это подробнее. Учет за один год равен:
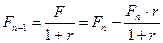
т.е. представляет собой разность между 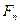 и процентами "на 100" по отношению к
и процентами "на 100" по отношению к 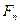 . Учет за два года равен:
. Учет за два года равен:
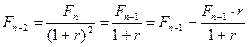 ,
,
т.е. представляет собой разность между 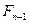 и процентами "на 100" по отношению к
и процентами "на 100" по отношению к 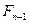 и т.д.
и т.д.
При 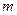 - кратном начислении процентов в год из (4.12) получим (обозначая
- кратном начислении процентов в год из (4.12) получим (обозначая 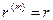 ):
):
 (4.22)
(4.22)
и соответственно
 (4.23)
(4.23)
Пример:
Из какого капитала можно получить 4 тыс. тенге через 5 лет наращением сложными процентами по ставке 12%, если наращение осуществлять: а) ежегодно; б) ежеквартально?
В данном случае  ,
, 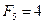 ,
, 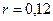 .
.
При ежегодном наращении пользуемся формулой (4.20) и приложением 3:
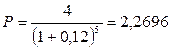 тыс. тенге. По формуле (4.21):
тыс. тенге. По формуле (4.21):
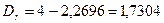 тыс. тенге
тыс. тенге
При ежеквартальном наращении пользуемся формулой (4.22), также можно воспользоваться приложением 3, определяя значение дисконтного множителя при  и числе периодов
и числе периодов 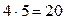 :
:
По формуле (4.23)
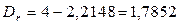 тыс. тенге
тыс. тенге
Обратим внимание, что если пользоваться непосредственно формулами (4.20), (4.22) и проводить вычисления с точностью до 0,0001, то получим для случаев а) и б) соответственно 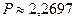 тыс. тенге и
тыс. тенге и 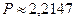 тыс. тенге. Отличие от значений, полученных с помощью приложения 3, объясняется точностью таблиц. Если значение дисконтного множителя в таблице будет с большим количеством знаков после запятой, то, естественно, и точность вычислений увеличится.
тыс. тенге. Отличие от значений, полученных с помощью приложения 3, объясняется точностью таблиц. Если значение дисконтного множителя в таблице будет с большим количеством знаков после запятой, то, естественно, и точность вычислений увеличится.
Используя формулы (4.20) и (4.22), можно приводить в сопоставимый вид оценку доходов от инвестиций, ожидаемых к поступлению в течение ряда лет. В этом случае процентная ставка в дисконтном множителе устанавливается инвестором и равна тому относительному размеру дохода, который инвестор хочет или может получить на инвестируемый им капитал.
Определяя процентную ставку в дисконтном множителе, обычно исходят из так называемого безопасного, или гарантированного уровня доходности финансовых инвестиций, который обеспечивается государственным банком по вкладам или при операциях с ценными бумагами. При этом может даваться надбавка за риск, причем, чем более рисковым считается рассматриваемый проект или финансовый контракт, тем больше размер премии за риск. Иными словами, процентная ставка 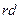 , используемая в дисконтном множителе, будет в этом случае иметь следующий вид:
, используемая в дисконтном множителе, будет в этом случае иметь следующий вид:
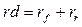 ,
,
где  - безрисковая доходность;
- безрисковая доходность;
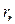 - премия за риск.
- премия за риск.
Пример:
На вашем счете в банке 20 тыс. тенге. Банк платит 18% годовых. Вам предлагают войти всем вашим капиталом в организацию венчурного предприятия. Представленные экономические расчеты показывают, что через шесть лет ваш капитал утроится. Стоит ли принимать это предложение?
Оценка данной ситуации может быть сделана либо с позиции будущего, либо с позиции настоящего. В первом случае анализ основан на сравнении двух сумм, получаемых от вложения в рисковое предприятие и в банковское учреждение с гарантированным доходом. Первая сумма равна 60 тыс. тенге, вторая находится по формуле (4.1):
 тыс. тенге
тыс. тенге
Приведенный расчет свидетельствует об экономической выгоде сделанного вам предложения. Однако при принятии окончательного решения необходимо по возможности учесть фактор риска.
Второй вариант анализа основан на дисконтированных оценках. Допустим, что финансовый консультант рекомендует оценить риск участия в венчурном предприятии путем введения премии в размере 5%. Таким образом, используемая в коэффициенте дисконтирования ставка будет равна 23%. Тогда по формуле (4.20) можно рассчитать приведенную стоимость 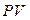 ожидаемого поступления при участии в венчурном предприятии:
ожидаемого поступления при участии в венчурном предприятии:
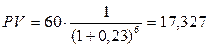 тыс. тенге
тыс. тенге
При таких исходных посылках предложение об участии в венчурном предприятии становится невыгодным.
Заметим, что при математическом учете можно использовать и равенства (4.6), (4.9) - (4.11), разрешенные относительно  . Например, из (4.6) получим:
. Например, из (4.6) получим:
 ,
,
т.е. за целое число лет осуществляется сложный учет "на 100", а затем полученная сумма учитывается из простых процентов "на 100". Аналогичным образом преобразуются и формулы (4.9) – (4.11).
Будущие поступления, являющиеся разновременными суммами, можно оценивать с позиции любого момента времени. Например, если через время 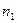 и
и  ожидаются выплаты сумм
ожидаются выплаты сумм  и
и  , но мы хотим их оценить, когда пройдет время, равное
, но мы хотим их оценить, когда пройдет время, равное  , то выплаты с позиции этого момента эквивалентны соответственно суммам
, то выплаты с позиции этого момента эквивалентны соответственно суммам
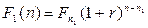 и
и 
Суммы  и
и  рассматриваются в один и тот же момент времени и, следовательно, их можно сравнивать между собой. Очевидно, если
рассматриваются в один и тот же момент времени и, следовательно, их можно сравнивать между собой. Очевидно, если 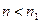 , то
, то  является приведенной стоимостью суммы
является приведенной стоимостью суммы  , а если
, а если 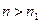 , то
, то  является наращенной суммой. То же самое можно сказать и про
является наращенной суммой. То же самое можно сказать и про  .
.
Можно доказать, что для случая сложных процентов и постоянной процентной ставки справедливо утверждение: если 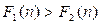 для некоторого значения
для некоторого значения 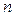 , то это неравенство справедливо и для любого
, то это неравенство справедливо и для любого 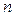 . Поэтому для сравнения
. Поэтому для сравнения  и
и  можно найти, например, их приведенные стоимости на текущий ("сегодняшний") момент времени.
можно найти, например, их приведенные стоимости на текущий ("сегодняшний") момент времени.
Пример:
Что выгоднее: получить 2,8 тыс. тенге через 3 года или 2,9 тыс. тенге через 4 года, если можно поместить деньги на депозит под сложную ставку 10% годовых?
Так как с позиции текущего момента:
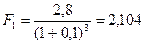 тыс. тенге,
тыс. тенге, 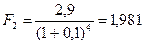 тыс. тенге,
тыс. тенге,
то выгоднее получить 2,8 тыс. тенге через 3 года.
Конечно, можно было проводить все сравнения с позиции будущего: через 4 года. Тогда определяем наращенную сумму за один год капитала 2,8 тыс. тенге: 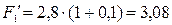 тыс. тенге и, сравнивая с 2,9 тыс. тенге, приходим к тому же выводу.
тыс. тенге и, сравнивая с 2,9 тыс. тенге, приходим к тому же выводу.
Сравним результаты математического дисконтирования по простой и сложной ставкам, обозначив  ,
, 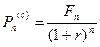 . Учитывая известные соотношения между
. Учитывая известные соотношения между  и
и 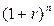 , можно написать:
, можно написать:
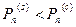 , если
, если 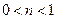 ;
;
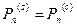 , если
, если 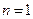 ;
;
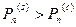 , если
, если 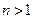 .
.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1350; Нарушение авторских прав?; Мы поможем в написании вашей работы!