Эквивалентность ставок

Мы уже не раз убеждались, что один и тот же финансовый результат можно получить разными способами, используя раз­личные ставки, методы наращения и дисконтирования. И это не удивительно, так как любая ставка (процентная, учетная или сила роста) характеризует доходность финансовой операции.

Две ставки называются эквивалентными, если при замене одной ставки на другую финансовые отношения сторон не ме­няются. Таким образом, участникам финансового соглашения безразлично, какая ставка будет фигурировать в контракте.

Соотношения между эквивалентными ставками уже приво­дились в первой главе (основные равенства (1.3)) и в главе, по­священной простым процентам (формула (2.22) и следствия из нее). Аналогичные соотношения получены при обсуждении эффективных процентной и учетной ставок (формулы (3.17), (3.18), (3.33), (3.34)), а также при сравнении силы роста и годо­вых ставок (формулы (3.42), (3.43)). Укажем и другие зависимо­сти между ставками, отражающие эквивалентность последних.

При выводе равенств, связывающих эквивалентные ставки, используется следующая идея: если из капитала PV наращени­ем за время n необходимо получить капитал FV, то будут эк­вивалентными все ставки, обеспечивающие один и тот же мно­житель наращения. Поэтому, приравнивая друг другу множите­ли наращения, получим соотношения между эквивалентными ставками. Точно так же при переходе от FV к PV с помощью дисконтирования приравниваются множители дисконтирования.

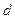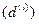
Обозначим через , соответственно процентную и учет­ную простые ставки; через , - процентную и учетную годовые номинальные ставки; через 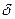- силу роста, а через - длительность финансовой сделки. Приравнивая соответствующие множители, получим ряд равенств, которые для наглядности разобьем на группы.

1. Эквивалентность простых и сложных ставок

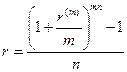(3.69)

(3.70)

(3.71)

(3.72)

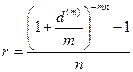(3.73)

Обратим внимание, что при п-\ формулы (3.69) и (3.70) совпадают с (3.17) и (3.18), а формулы (3.71) и (3.72) — с (3.33) и (3.34).

Пример

Предлагается поместить капитал на 4 года либо под сложную процентную ставку 20% с полугодовым начислением процентов, либо под простую процентную ставку 26% годовых. Выяснить,

как выгоднее поступить.

Чтобы сделать правильный выбор, необходимо найти для данной сложной процентной ставки 20% эквивалентную про­стую процентную ставку и сравнить ее с предлагаемой простой процентной ставкой 26%. Используем формулу (3.69):

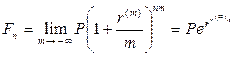
Дата добавления: 2014-01-05