Приведение общего уравнения плоскости к нормальному виду

Отклонения и расстояние от точки до плоскости в пространстве

Расстоянием от точки до плоскости, называется длина перпендикулятора, опущенная из этой точки на плоскость

Отклонением точки до плоскости называется расстояние взятое со знаком «+», если начало координат и точка находящаяся по разные стороны от плоскости и со знаком «-».

Теорема: Отклонение точки до плоскости равно левой части нормального уравнения. Для того, чтобы вычислить расстояние, нужно уравнение плоскости привести к нормальному уравнению.

Ax + By + Cz + D = 0

x cos£ + y cosβ + z cosγ – p = 0

Оба уравнения определяют одну и ту же плоскость, а значит должно найтись такое λ, которое уравнит коэффициенты

λA = cos£ - все части возводим в квадрат и складываем

λB = cosβ

λC = cosγ

λD = - p

λ² = (A²+B²+C²)==>cos²£ + cos²β + cos²γ = 1

λ² =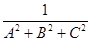

λ = ±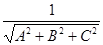

Формула 16.11 позволяет вычислить множитель λ. Λ называется нормирующим множителем, знак который выбирается противополдожный знаку свободного члена общего уравнения.

Для того, чтобы общее уравнение плоскости привести к нормальному виду. Все члены общего уравнения умножить на нормирующий множитель.

§ 17. Прямая в пространстве.

17.1 Общее уравнение прямой в пространстве.

Прямая в пространстве рассматривается как пересечение двух плоскостей

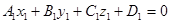– общее уравнение прямой в пространстве

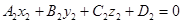
17.2. Кононическое уравнение в пространстве.

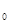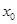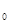Пусть имеется 1 точка М(;y; z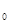), 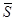(m; n; p)

Через данную точку, параллельную данному вектору можно провести единственную прямую l. Требуется составить уравнение этой прямой.

Введем любую точку М (x; y; z) 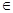l. Для всех точек, лежащих на прямой l будет выполняться коллинеарность векторов.

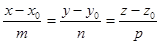- кононическое уравнение (17.2)

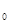£. М М

Дата добавления: 2014-01-05