Типы комбинаторных задач

Типы комбинаторных проблем

Проблемы и задачи комбинаторики

Лекция 1.

Комбинаторика изучает приёмы нахождения числа различных комбинаций, составленных из данных предметов (элементов дискретного множества предметов) при определённых условиях.

Комбинация – некоторое сочетание предметов.

1. Проблемы существования. Доказывается теоретически, что есть решение или нет.

2. Если решения задачи есть, то сколько их.

3. Выбрать наиболее экономичный способ решения.

1. Задача о маршрутах.

2. Задача о размещении.

3. Задача о покрытии.

4. Задача об укладке.

5. Задача о разбиении.

Все остальные задачи представляют собой объединение, пересечение, произведение указанных типов задач.

Пусть S – множество из n элементов (| S|=n). Говорят, что S – n -множество.

T ₁ T₂   T_n

Задача о покрытии

Найти такие множества T_i, i = 1, 2, …, r, чтобы 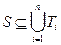(чтобы объединение этих множеств «покрыло» S). Например, застелить весь пол в комнате несколькими коврами. Ковры могут накладываться друг на друга (множества могут пересекаться), но незакрытых участков пола быть не должно.

Во многих задачах покрытие должно быть наиболее экономичным (так называемое минимальное покрытие), когда число множеств T_i должно быть минимальным, сами они должны содержать минимально возможное число элементов.

Задача о укладке

Найти такие попарно непересекающиеся множества T_i, i = 1, 2, …, r, (T_i Ç T_j = Æ при i ¹ j) чтобы 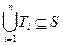(чтобы объединение этих множеств вошло в S). (нарисовать)

Например, уложить несколько предметов в одну коробку. Между предметами могут быть пустые промежутки, но сами предметы друг с другом не пересекаются и укладываются в коробку.

Во многих задачах укладка должна быть наиболее экономичной, когда укладывается максимально возможное количество предметов, а количество пустых промежутков должно быть как можно меньше.

Задача о разбиении

Найти такие попарно непересекающиеся множества T_i, i = 1, 2, …, r, (T_i Ç T_j = Æ при i ¹ j) чтобы 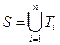(чтобы объединение этих непересекающихся множеств дало S). (нарисовать)

Например, группы в институте – это разбиение множества студентов института. Группы не пересекаются, а их объединение дает множество всех студентов института.

Дата добавления: 2014-01-05