Основные понятия и аксиомы. Определение натурального числа

В качестве основного понятия при аксиоматическом построении арифметики натуральных чисел взято отношение «непосредственно следовать за», заданное на непустом множестве N. Известными также считаются понятие множества, элемента множества и другие теорети­ко-множественные понятия, а также правила логики.

Элемент, непосредственно следующий за элементом а, обозначают а'.

Суть отношения «непосредственно следовать за» раскрывается в следующих аксиомах.

Аксиома 1. В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Будем назы­вать его единицей и обозначать символом 1.

Аксиома 2. Для каждого элемента а из N существует единствен­ный элемент а ¢, непосредственно следующий за а.

Аксиома 3. Для каждого элемента а из N существует не более од­ного элемента, за которым непосредственно следует а.

Аксиома 4. Всякое подмножество М множества N совпадает с N, если обладает свойствами: 1) 1 содержится в М; 2) из того, что а со­держится в М, следует, что и а' содержится в М.

Сформулированные аксиомы часто называют аксиомами Пеано.

Используя отношение «непосредственно следовать за» и аксиомы 1-4, можно дать следующее определение натурального числа.

Определение. Множество N, для элементов которого установ­лено отношение «непосредственно следовать за», удовлетворяю­щее аксиомам 1-4, называется множеством натуральных чисел, а его элементы - натуральными числами.

В данном определении ничего не говорится о природе элементов множества N. Значит, она может быть какой угодно. Выбирая в качестве множества N некоторое конкретное множество, на котором зада­но конкретное отношение «непосредственно следовать за», удовле­творяющее аксиомам 1-4, мы получим модель данной системы аксиом. В математике доказано, что между всеми такими моделями можно установить взаимно однозначное соответствие, сохраняющее отноше­ние «непосредственно следовать за», и все такие модели будут отли­чаться только природой элементов, их названием и обозначением. Стандартной моделью системы аксиом Пеано является возникший в процессе исторического развития общества ряд чисел:

1,2,3,4,...

Каждое число этого ряда имеет свое обозначение и название, кото­рое мы будем считать известными.

Рассматривая натуральный ряд чисел в качестве одной из моделей аксиом 1-4, следует отметить, что они описывают процесс образова­ния этого ряда, причем происходит это при раскрытии в аксиомах свойств отношения «непосредственно следовать за». Так, натураль­ный ряд начинается с числа 1 (аксиома 1); за каждым натуральным числом непосредственно следует единственное натуральное число (аксиома 2); каждое натуральное число непосредственно следует не более чем за одним натуральным числом (аксиома 3); начиная от чис­ла 1 и переходя по порядку к непосредственно следующим друг за другом натуральным числам, получаем все множество этих чисел (аксиома 4). Заметим, что аксиома 4 в формализованном виде описыва­ет бесконечность натурального ряда, и на ней основано доказательст­во утверждений о натуральных числах.

Вообще моделью системы аксиом Пеано может быть любое счет­ное множество, например:

I, II, III, IIII,...

о, оо, ооо, оооо, …

один, два, три, четыре, …

Рассмотрим, например, последовательность множеств, в которой множество {оо} есть начальный элемент, а каждое последующее мно­жество получается из предыдущего приписыванием еще одного круж­ка (рис. 108,а). Тогда N есть множество, состоящее из множеств опи­санного вида, и оно является моделью системы аксиом Пеано. Дейст­вительно, в множестве N существует элемент {оо}, непосредственно не следующий ни за каким элементом данного множества, т.е. вы­полняется аксиома 1. Если счи­тать обведенные кружки за один элемент (рис. 108.6), то для каждого

а) {о о}, {о о о}, {о о о о}, …

б) { }, { о}, { о о}, …

Рис. 108

Рис. 109

множества А рассматриваемой совокупности существует единст­венное множество, которое получается из А добавлением одного круж­ка, т.е. выполняется аксиома 2. Для каждого множества А существует не более одного множества, из которого образуется множество А добавле­нием одного кружка, т.е. выполняется аксиома 3. Если М Ì N и из­вестно, что множество А содержится в М, следует, что и множество, в котором на один кружок больше, чем в множестве А, также содер­жится в N, то М ~ N (и значит, выполняется аксиома 4).

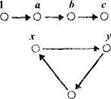
Заметим, что в определении натурального числа ни одну из аксиом опустить нельзя - для любой из них можно построить множество, в котором выполнены остальные три аксиомы, а данная аксиома не вы­полняется. Это положение наглядно подтверждается примерами, приве­денными на рисунках 109 и 110. На рисунке 109, а) изображено множе­ство, в котором выполняются аксиомы 2 и 3, но не выполнена ак­сиома 1 (аксиома 4 не будет иметь смысла, так как в множестве нет эле­мента, непосредственно не следующего ни за каким другим). На рисун­ке 109, 6) показано множество, в котором выполнены аксиомы 1, 3 и 4, но за элементом а непосредственно следуют два элемента, а не один, как требуется в аксиоме 2. На рисунке 109, в) изображено множество, в котором выполнены аксиомы 1, 2, 4, но элемент с непосредственно следует как за элементом а, так и за элементом b. На рисунке 110 пока­зано множество, в котором выполнены аксиомы 1, 2, 3, но не выпол­няется аксиома 4 - множество точек, лежащих на луче, содержит 1 и вместе с

Рис. 110

каждым числом оно содержит непосредственно следующее за ним чис­ло, но оно не совпадает со всем множест­вом точек, показанных на рисунке.

То обстоятельство, что в аксиомати­ческих теориях не говорят об «истинной» природе изучаемых понятий, делает на первый взгляд эти теории слишком абстрактными и формальными, - оказывается, что одним и тем же аксиомам удовлетворяют различные множества объектов и разные отношения между ними. Однако в этой кажущейся абстрактности и состоит сила аксиоматического метода: каждое утверждение, выведенное логиче­ским путем из данных аксиом, применимо к любым множествам объ­ектов, лишь бы в них были определены отношения, удовлетворяющие аксиомам.

Итак, мы начали аксиоматическое построение системы натураль­ных чисел с выбора основного отношения «непосредственно следо­вать за» и аксиом, в которых описаны его свойства. Дальнейшее по­строение теории предполагает рассмотрение известных свойств нату­ральных чисел и операций над ними. Они должны быть раскрыты в определениях и теоремах, т.е. выведены чисто логическим путем из отношения «непосредственно следовать за», и аксиом 1-4.

Первое понятие, которое мы введем после определения натураль­ного числа, - это отношение «непосредственно предшествует», кото­рое часто используют при рассмотрении свойств натурального ряда.

Определение. Если натуральное число b непосредственно следует за натуральным числом а, то число а называется непосредствен­но предшествующим (или предшествующим) числу b.

Отношение «предшествует» обладает рядом свойств. Они форму­лируются в виде теорем и доказываются с помощью аксиом 1-4.

Теорема 1. Единица не имеет предшествующего натурального числа.

Истинность данного утверждения вытекает сразу из аксиомы 1.

Теорема 2. Каждое натуральное число а, отличное от 1, имеет предшествующее число b, такое, что b ' = а.

Доказательство. Обозначим через М множество натуральных чисел, состоящее из числа 1 и из всех чисел, имеющих предшествую­щее. Если число а содержится в М, то и число а' также есть в N, по­скольку предшествующим для а' является число а. Это значит, что множество М содержит 1, и из того, что число а принадлежит множе­ству М, следует, что и число а' принадлежит М. Тогда по аксиоме 4 множество М совпадает с множеством всех натуральных чисел. Зна­чит, все натуральные числа, кроме 1, имеют предшествующее число.

Отметим, что в силу аксиомы 3 числа, отличные от 1, имеют един­ственное предшествующее число.

Аксиоматическое построение теории натуральных чисел не рас­сматривается ни в начальной, ни в средней школе. Однако те свойства отношения «непосредственно следовать за», которые нашли отраже­ние в аксиомах Пеано, являются предметом изучения в начальном курсе математики. Уже в первом классе при рассмотрении чисел пер­вого десятка выясняется, как может быть получено каждое число. При этом используются понятия «следует» и «предшествует». Каждое новое число выступает как продолжение изученного отрезка натураль­ного ряда чисел. Учащиеся убеждаются в том, что за каждым числом идет следующее, и притом только одно, что натуральный ряд чисел бесконечен. И конечно, знание аксиоматической теории поможет учителю методически грамотно организовать усвоение детьми особенности натурального ряда чисел.

Дата добавления: 2014-01-06