Свойства пересечения и объединения множеств

Лекция № 4

Из школьного курса математики известно, что операцию, при помощи которой находят сумму чисел, называют сложением. Выполняют и другие операции над числами: вычитание, умножение, деление. При этом результаты этих операций называют соответственно разностью, произведением, частным. Для рассмотренных операций над множествами, ситуация другая: операции, при помощи которых находят пересечение и объединение, называют соответственно пересечением и объединением.

Известно так же, что операции над числами обладают рядом свойств. Например, переместительное и сочетательное свойства сложения: а+в=в+а и (а+в)+с=а+(в+с). Аналогичными свойствами обладает умножение.

Выясним, обладают ли похожими свойствами пересечение и объединение множеств.

Если обратиться к пересечению и объединению множеств, то можно увидеть, что в них не фиксируется порядок оперирования множествами (при объединении к элементам одного множества можно присоединить элементы другого, а можно поступить наоборот) – это означает, что пересечение и объединение обладают переместительным (или коммутативным) и сочетательным (или ассоциативным) свойством.

Свойства пересечения:

1. Коммутативность: А∩В = В∩А

2. Ассоциативность:

(А∩В)∩С =А∩(В∩С)

3. АÌВ => А∩В =А

4. А∩Ø = Ø

5. А∩U =A

6. А∩А = А

Свойства объединения:

1. Коммутативность: AÈB = BÈA

2. Ассоциативность:

(AÈB)ÈC =AÈ(BÈC)

3. AÌB => AÈB = B

4. AÈØ =A

5. AÈU = U

6. AÈA = A

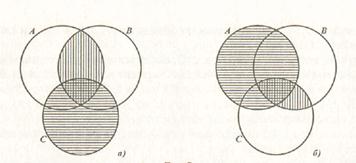
Проиллюстрируем с помощью кругов Эйлера ассоциативное свойство пересечения множеств. Изобразим множества А, В и С в виде трех попарно пересекающихся кругов.

Видим, что области, представляющие множества (А∩В)∩С и А∩(В∩С), одинаковы, что и подтверждает справедливость свойства ассоциативности для пересечения множеств.

Аналогично можно показать свойство ассоциативности и для объединения множеств.

Взаимосвязь пересечения и объединения множеств отражается в распределительных или дистрибутивных свойствах этих операций. Таких свойств два:

1. Пересечение дистрибутивно относительно объединения множества, т.е. для любых множеств А, В и С выполняется равенство:

(А È В) ∩ С = (А ∩ С) È (В ∩ С)

2. Объединение дистрибутивно относительно пересечения множеств, т.е. для любых множеств А, В и С выполняется равенство:

(А ∩ В) È C = (А È C) ∩ (В È C).

Замечание. Если в выражении есть знаки пересечения и объединения множеств и нет скобок, то сначала выполняют пересечение, так как считают, что пересечение более «сильная» операция, чем объединение. Поэтому в записи дистрибутивного свойства пересечения относительно объединения можно опустить скобки в правой части равенства.

Если провести аналогию с действиями над числами, то можно увидеть, что дистрибутивное свойство пересечения относительно объединения сопоставимо с распределительным свойством умножения относительно сложения, при условии, что в качестве операций, аналогичной пересечению, рассматривают умножение, а для объединения – сложение. Но для дистрибутивного свойства объединения множеств относительно пересечения аналогичного свойства над числами нет.

Понятие пересечения и объединения множеств можно обобщить на любое конечное число множеств:

А₁ ∩ А₂ ∩ А₃ ∩ …∩А_n = { x ÷ x ÎA₁ и x ÎA₂ и…и x ÎA_n},

A₁ È A₂ È A₃ È …ÈA_n= { x ÷ x ÎA₁ или x ÎA₂ или … x ÎA_n}.

Аналогично можно поступить и по отношению к рассмотренным свойствам данных операций.

Дата добавления: 2014-01-06