Неявно и параметрически

Дифференцирование функций, заданных

III уровень

3.1. Вычислите значение 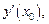если:

1)

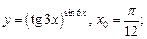
2)

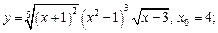
3)

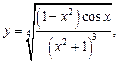
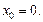
3.2. Запишите уравнение касательной и нормали к графику функции в указанной точке:

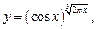
1) 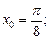2)

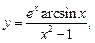
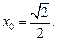
Уравнение

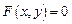(17.4)

задает неявно функцию 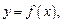если при подстановке выражения f (x) вместо y в уравнение (17.4) оно превращается в тождество. Предположим, что функция 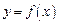дифференцируема и требуется вычислить производную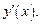

Первый способ. Если практически возможно, выражают y через x и дифференцируют y (x) по правилам дифференцирования.

Второй способ. Дифференцируют уравнение (17.4) по x, считая, что y есть функция от x. Получают новое уравнение, содержащее x, y и 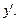Из него находят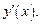

Пусть функция 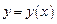задана параметрически уравнениями:

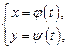
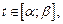(17.5)

где функци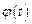и и 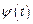дифференцируемы для любого 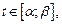причем 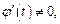и требуется найти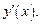

Первый способ. Из первого уравнения системы (17.5) выражают t через x (если это возможно) и подставляют во второе уравнение системы (17.5). Приходят к сложной функции от переменной x, которую дифференцируют по x.

Второй способ. Используют формулу

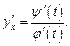(17.6)

Полученное таким образом выражение для 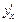зависит от переменной t. Если возможно (и необходимо) из первого уравнения системы (17.5) выражают t через х и подставляют в выражение, полученное для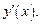

Задания

Дата добавления: 2014-01-06