
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нормальное распределение. Нормальным называют распределение вероятностей непрерывной
|
|
|
|
Нормальным называют распределение вероятностей непрерывной
случайной величины, которое описывается плотностью
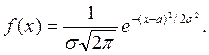
Видим, что нормальное распределение определяется двумя параметрами: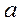 и
и 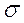 .
.
Покажем, что вероятностный смысл этих параметров: 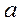 есть
есть
математическое ожидание, 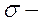 среднее квадратическое отклонение нормального распределения.
среднее квадратическое отклонение нормального распределения.
а) По определению математического ожидания непрерывной случайной величины,

Для интегрирования вводим новую переменную 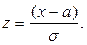 Отсюда
Отсюда 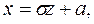
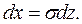 Новые пределы интегрирования остаются равными старым. Получим
Новые пределы интегрирования остаются равными старым. Получим

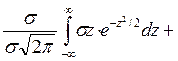

В этом выражении первый интеграл равен нулю, т.к. под знаком интеграла нечетная функция. Второе из слагаемых равна 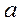 , т.к. интеграл Пуассона
, т.к. интеграл Пуассона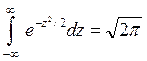 . Следовательно,
. Следовательно, 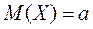 .
.
Математическое ожидание нормального распределения равно параметру распределения 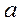 .
.
б) По определению дисперсии непрерывной случайной величины, учитывая, что 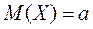 , имеем
, имеем
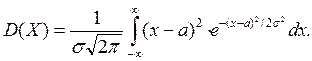
Введем новую переменную 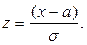 Отсюда
Отсюда 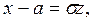

При этом пределы интегрирования не меняются и получим

Интегрируя по частям, положив 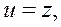
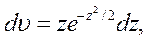
найдем
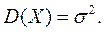
Итак, среднее квадратическое отклонение нормального распределения равна параметру 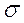 распределения.
распределения.
Замечание. Общим называют нормальное распределение с произвольными параметрами 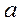 и
и 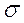 .
.
Нормированным называют нормальное распределение с параметрами 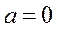 и
и 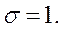 Например, если
Например, если  - нормальная величина с параметрами
- нормальная величина с параметрами 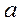 и
и 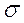 , то
, то  - нормированная нормальная величина, причем
- нормированная нормальная величина, причем 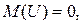
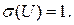 Плотность нормированного распределения
Плотность нормированного распределения
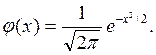
Эта функция табулирована и приводится в приложениях учебников.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 321; Нарушение авторских прав?; Мы поможем в написании вашей работы!