Нормальная кривая

Исследуем функцию

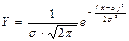
которая задает плотность вероятности нормального закона распределения случайной величины X. График этой функции называется нормальной кривой (кривой Гаусса). Рассмотрим свойства этой функции.

1. Функция определена на всей числовой оси x.

2. При всех значениях x функция принимает положительные значения, нормальная кривая расположена над осью x.

3. Предел функции при неограниченном возрастании x (по абсолютной величине) равен нулю, т.е. ось x служит горизонтальной асимптотой графика.

4. Исследуем функцию на экстремум. Найдем производную

Первый сомножитель 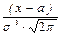обращается в нуль при x = a. Поэтому y = 0 при x = a, Y ¢ > 0 при x < a, Y ¢ < 0 при x > a. Следовательно, при x = a функция имеет максимум, равный .

5. Функция содержит разность (x – a) в квадрате, т.е. график функции симметричен относительно прямой x = a.

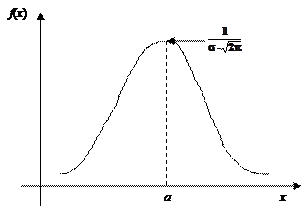
Дата добавления: 2014-01-06