Лекция 2. Элементы кинематики

Механика и ее разделы. Физические модели: материальная точка (частица), абсолютно твердое тело (система материальных точек), сплошная среда. Понятие состояния в механике. Пространственно-временные отношения. Развитие представлений о свойствах пространства и времени в механике. Системы отсчета и описание движений. Элементы кинематики материальной точки: перемещение, скорость и ускорение. Элементы кинематики материальной точки и тела, совершающих вращательное движение: угол поворота, угловые скорость и ускорение. Их связь с линейной скоростью и линейным ускорением. Гармонические колебательные движения и их характеристики: смещение, амплитуда, период, частота, фаза, скорость и ускорение. Методы сложения гармонических колебаний. Векторные диаграммы. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.

2.1. Механика и ее разделы. Физические модели: материальная точка (частица), абсолютно твердое тело (система материальных точек), сплошная среда

Механика – раздел физики, в котором изучается простейшая форма движения - механическое движение, причины вызывающие это движение и происходящие при этом взаимодействия между телами.

Механическое движение - изменение с течением времени взаимного положения тел или их частей (частиц) в пространстве. В природе - движение небесных тел, колебания земной коры, воздушные и морские течения и т.д. В технике - движение различных летательных аппаратов и транспортных средств, машин и механизмов, деформации элементов различных конструкций и сооружений, движение жидкостей и газов.

В соответствии с характером решаемых задач механику подразделяют на следующие разделы: 1) кинематику; 2) динамику; 3) статику.

Кинематика изучает геометрические свойства движения и взаимодействия тел в не связи с порождающими их причинами.

Динамика изучает движение и взаимодействия тел совместно с причинами, обусловливающими тот или иной характер движения и взаимодействия.

Статика изучает равновесие тел, систем под действием сил.

При изучении различных движений и взаимодействий в классической механике вводят в рассмотрение физические модели или научные абстракции, основными из которых являются:

1. Материальная точка - объект малых размеров (размерами, которого в условиях данной задачи можно пренебречь), обладающий массой. Это понятие применимо, когда тело движется поступательно или когда в изучаемом движении можно пренебречь вращением тела вокруг его центра масс;

2. Абсолютно твердое тело - тело, расстояние между двумя любыми точками которого всегда остается неизменным. Применимо, когда можно пренебречь деформацией тела;

3. Сплошная изменяемая среда. Понятие применимо при изучении движения изменяемой среды (деформируемого твердого тела, жидкости, газа), когда можно пренебречь молекулярной структурой среды.

При изучении сплошных сред вводят такие абстракции, которые отражают при данных условиях наиболее существенные свойства реальных тел: идеально упругое тело, пластичное тело, идеальная жидкость, вязкая жидкость, идеальный газ и др.

В соответствии с вводимыми научными абстракциями (моделями) различают: а) механику материальной точки; б) механику системы материальных точек; в) механику абсолютно твердого тела; г) механику сплошной среды (теорию упругости, теорию пластичности, гидродинамику, аэродинамику, газовую динамику).

2.2. Пространственно-временные отношения. Развитие представлений о свойствах пространства и времени в механике

Пространство и время – категории, обозначающие основные формы существования и взаимодействия объектов.

Пространство выражает порядок существования объектов. Время -порядок смены событий.

Пространство и время - основные понятия всех разделов физики. Они играют важную роль на эмпирическом уровне физического познания. Непосредственное содержание результатов наблюдений и экспериментов состоит в фиксации пространственно - временных совпадений. Они служат также одними из важнейших средств конструирования теоретических моделей, интерпретирующих экспериментальные данные.

Для построения физической картины мира понятия пространство и время, обеспечивая отождествление и различие (индивидуализацию) отдельных фрагментов материальной действительности, имеют решающее значение.

Различают метрические (протяженность и длительность) и топологические (размерность, непрерывность и связанность, порядок и направление времени) свойства пространства и времени.

Современными теориями метрических свойств пространства и времени являются: специальная теория относительности (СТО) и общая теория относительности (ОТО).

Исследование топологических свойств пространства и времени в физике было начато в 60 - 70-х годах двадцатого столетия и пока не вышло из стадии гипотез.

Историческое развитие физических представлений о пространстве и времени проходило по двум направлениям в тесной связи с различными философскими представлениями.

В основе одного из них лежали идеи Демокрита, приписывающие пустоте особый род бытия. Они нашли наиболее полное физическое воплощение в понятиях абсолютного пространства и времени И. Ньютона. Согласно И. Ньютону абсолютное пространство и время представляют собой самостоятельные сущности, которые не зависят друг от друга, и от находящихся в них материальных объектов и протекающих в них процессов.

Другое представление о пространстве и времени заложено в учении Аристотеля, которое было разработано в философских работах Г.В. Лейбница, трактовавшего пространство и время как определенные типы отношений между объектами и их изменениями, не имеющие самостоятельного существования. В физике концепция Г.В. Лейбница была развита А. Эйнштейном в теории относительности.

2.3. Системы отсчета и описание движений. Элементы кинематики материальной точки: перемещение, скорость и ускорение

Известно, что кинематика - это учение о геометрических свойствах движения и взаимодействия тел, или раздел механики, в котором изучаются движения и взаимодействия тел в не связи с причинами, их порождающими. Изучается простейший вид движения - механическое движение. Это процесс изменения положения физических тел или их частей по отношению к другим телам или частям одного и того же тела в пространстве и во времени. Поэтому механическое движение всегда относительно.

Произвольно выбранное, условно неподвижное тело, по отношению к которому рассматривается движение данного тела, называют телом отсчета.

Связанная с телом отсчета произвольная система координат называется системой отсчета.

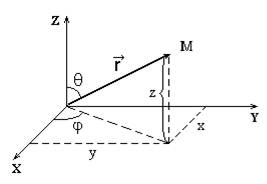Рис.2.1

В качестве тела отсчета чаще всего выбирают Землю или любое другое тело, неподвижное или движущееся относительно Земли, системы отсчета - прямоугольную, трехмерную (декартову) систему координат, в точке пересечения осей которой помещают тело отсчета. Для задания положения материальной точки применяется также полярная система координат.

На рис. 2.1 показана прямоугольная (декартова) система координат.

Положение материальной точки (тела) в прямоугольной системе отсчета, в данный момент времени, может быть определено тремя способами: 1) с помощью координат x, y, z - M(x,y,z). В этом случае говорят, что материальная точка обладает тремя степенями свободы; 2) с помощью радиус - вектора r; 3) естественным (траекторным), который применяется обычно тогда, когда известна траектория движения точки по отношению к выбранной системе отсчета. В этом случае зависимость S = f(t) может быть задана графически либо в виде таблицы. При этом указанные способы равноправны.

Между координатами x, y, z и проекциями радиус-вектора r существует связь:

x = r_x, y = r_y, z = r_z. (2.1)

С течением времени может произойти изменение положения материальной точки (тела) в пространстве (изменение ее координат), тогда можно записать:

x = f₁(t); y = f₂(t); z = f₃(t); (2.2)

r_x = f₁(t); r_y = f₂ (t); r_z = f₃(t). (2.3)

Записанные выражения являются уравнениями движения материальной точки (тела) в кинематике.

Совокупность последовательных положений материальной точки (тела) в процессе ее движения называют траекторией движения. Для определения (нахождения) уравнения траектории движения необходимо из уравнений движения исключить время.

Положение материальной точки в полярной системе координат задается радиус-вектором , который имеет определенный модуль r, и углами q и j, которые он составляет с осями декартовой системы координат.

С точки зрения кинематики, никакого различия между различными системами отсчета нет, и все они равноправны.

Простейшим видом механического движения тела является поступательное движение. Это такое движение, при котором тело перемещается параллельно самому себе. При этом все точки тела описывают одинаковые траектории, смещенные относительно друг друга. Рассматривая движение отдельных точек, можно установить характер движения тела.

Для характеристики движения материальной точки вводятся следующие основные понятия и определения.

Перемещение - вектор, проведенный из начального положения материальной точки (тела) в ее положение в данный момент времени (отрезок, соединяющий последовательные положения материальной точки или тела) - приращение радиус-вектора r за рассматриваемый промежуток времени

D r = r – r_о. (2.4)

Рис.2.2

Перемещение характеризуется не только численным значением, но и направлением в пространстве. На рис.2.2 D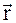– вектор перемещения точки за промежуток времени Dt: 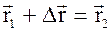или 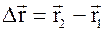; DS – пройденный за это время путь.

В общем случае перемещение не совпадает с траекторией движения. Достаточно малое перемещение, которое с достаточной степенью точности совпадает с соответствующим участком траектории движения, называют элементарным перемещением - d r.

При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения численно равен пройденному пути:

½D r ½ = DS (2.5)

Расстояние - модуль перемещения. Расстояние, пройденное телом при его движении по траектории, - путь. В частных случаях перемещение и путь могут совпадать.

За одни и те же промежутки времени перемещение точки может быть разным. Если положение точки в пространстве в какой-то момент времени t определить вектором r (t), а в момент времени t + Dt - (r + D r), то за время (t₂ – t₁) = Dt она совершает перемещение D r. При этом отношение D r /Dt зависит от Dt. Однако при уменьшении Dt эта зависимость становится менее явной, и при Dt®0 оно стремится к некоторому пределу. Предел отношения D r /Dt при Dt®0 называют мгновенной скоростью.

Таким образом, мгновенная линейная скорость - векторная физическая величина, характеризующая состояние движения, показывающая, как изменяется перемещение в единицу времени, численно равная первой производной от перемещения по времени:

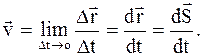(2.6)

Скоростью определяется как "быстрота" движения, так и его направление. При неравномерном движении модуль мгновенной скорости с течением времени может изменяться. В этом случае пользуются понятием средней скорости движения.

Средняя скорость неравномерного движения - скалярная физическая величина, численно равная отношению всего пути, пройденного телом (материальной точкой), к тому промежутку времени, в течение которого совершалось движение:

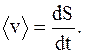(2.7)

Важной задачей кинематики является нахождение пройденного материальной точкой пути. Известно, что при прямолинейном равнопеременном движении

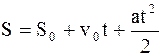. Согласно (2.6), 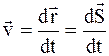, следовательно

d S = v× dt. (2.8)

При небольших промежутках времени Dt можно считать, что элементарный путь dS численно равен ½d r ½, причем при уменьшении промежутка времени точность совпадения числовых значений пути и перемещения возрастает.

Рис.2.3

Поэтому путь, пройденный материальной точкой при неравномерном движении за промежуток времени от t₁ до t₂, можно определить по формуле

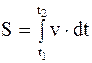. (2.9)

Таким образом, величина пути определяется криволинейным интегралом.

Это дает право представлять величину пройденного телом пути площадью фигуры, ограниченной кривой зависимости v = f(t), прямыми t = t₁,

t = t₂ и осью времени на графике скорости (рис.2.3).

В общем случае найти уравнение пути - означает определить зависимость координат от времени: 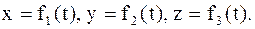При движении скорость материальной точки (тела) может изменяться как по величине, так и по направлению. Отношение изменения скорости D v к промежутку времени Dt, в течение которого оно происходит, зависит от величины Dt, однако при его уменьшении эта зависимость становится менее явной, и при Dt®0 оно стремится к пределу, который называют линейным ускорением:

. (2.10)

Следовательно, линейное ускорение - векторная физическая величина, характеризующая изменение скорости в единицу времени, численно равная первой производной от скорости или второй производной от перемещения по времени.

В общем случае вектор линейного ускорения не совпадает с вектором линейной скорости. Можно разложить вектор линейного ускорения на две составляющие по направлению линейной скорости - вдоль касательной к траектории движения. Эту составляющую линейного ускорения называют тангенциальным ускорением – а _t. Тангенциальное ускорение изменяет линейную скорость только по величине:

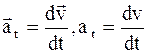. (2.11)

Составляющую линейного ускорения, направленную по нормали n к вектору линейной скорости, т.е. к касательной в данной точке, называют нормальным ускорением - a _n. Нормальное ускорение изменяет линейную скорость только по направлению:

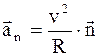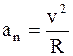, (2.12)

где R - радиус кривизны траектории движения;

n - единичный вектор нормали к траектории движения.

Полное ускорение a можно определить как

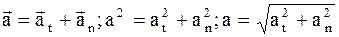. (2.13)

Таким образом, направление тангенциального ускорения всегда совпадает с направлением линейной скорости, а направление нормального ускорения перпендикулярно направлению линейной скорости.

При неравномерном движении величину

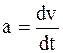(2.14)

называют мгновенным ускорением, а

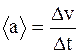(2.15)

-средним ускорением.

Надо отметить, что при поступательном движении тела все его точки имеют одинаковые линейные скорости и ускорения и описывают одинаковые траектории, смещенные относительно друг друга.

2.4. Элементы кинематики материальной точки и тела, совершающих вращательное движение: угол поворота, угловые скорость и ускорение. Их связь с линейной скоростью и линейным ускорением

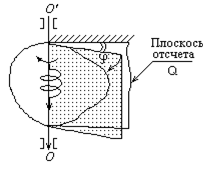Рис.2.4

Вращательным движением твердого тела вокруг неподвижной оси вращения называют такое движение, при котором какие-либо две его точки остаются неподвижными в процессе движения. Прямая, проходящая через эти точки, называется осью вращения; все остальные точки твердого тела при вращательном движении описывают окружности в плоскостях, перпендикулярных к оси вращения, центры которых лежат на этой оси (рис.2.4).

Основными кинематическими характеристиками вращательного движения являются: угол поворота, угловая скорость и угловое ускорение.

Угол поворота j - угол между проведенными через ось вращения неподвижной полуплоскостью (плоскостью отсчета) и полуплоскостью, жестко связанной с телом и вращающейся вместе с ним. Угол поворота - псевдовектор - вектор, численно равный углу между двумя положениями радиуса R, направленный вдоль оси вращения и связанный с направлением вращения правилом векторного произведения (правилом правого винта).

С определенной степенью точности, под углом поворота можно подразумевать псевдовектор, численно равный углу, отсчитанному между двумя последовательными положениями радиус-вектора r, и связанный с направлением вращения правилом правого винта.

Угловая скорость w - векторная физическая величина, показывающая, как изменяется угол поворота j в единицу времени, численно равная первой производной от угла поворота по времени:

. (2.16)

Вектор угловой скорости направлен вдоль оси вращения в сторону, определяемую правилом правого винта (векторного умножения).

При равномерном вращении ω = const, ω = φ/t. Равномерное вращательное движение характеризуется периодом, частотой вращения и циклической или круговой частотой.

Период (T) - время, в течение которого тело сделает один полный оборот.

Частота (n) - число оборотов, совершаемых в единицу времени.

Круговая (циклическая) частота ω - число оборотов, совершаемых за время, равное 2π. Между периодом, частотой и круговой частотой имеется связь:

ω = 2πn = 2π/T; n = 1/T. (2.17)

Угловая скорость может изменяться как по величине, так и по направлению. Векторная физическая величина, характеризующая изменению угловой скорости в единицу времени, численно равная первой производной от угловой скорости по времени или второй производной от угла поворота по времени, называется угловым ускорением

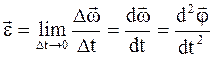. (2.18)

Направление вектора углового ускорения совпадает с направлением вектора угловой скорости в случае ускоренного вращения и противоположно - в случае замедленного.

Отдельные точки вращающегося тела имеют различные линейные скорости, которые непрерывно изменяют свое направление и зависят от угловой скорости w и расстояния соответствующей точки до оси вращенияr.

Точка, находящаяся на расстоянии r от оси вращения, двигаясь по траектории (окружности), проходит путь (рис.2.5):

Рис.2.5

DS = r×Dj. (2.19)

Поделив обе части данного равенства на Dt; при Dt®0 получим некоторые пределы от левой и правой частей:

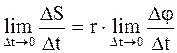или 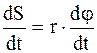. (2.20)

Так как dS/dt = v, а dφ/dt = ω, то

v = r×ω. (2.21)

Полученная формула устанавливает связь между численными значениями линейной и угловой скорости, а также радиус-вектором r. Из нее видно, чем дальше отстоит точка от оси вращения, тем больше ее линейная скорость. Векторы v, ω и r перпендикулярны друг другу, следовательно, можно записать:

v = r×ω sinα или v =[ ω × r ]. (2.22)

Известно, что a² = a_t² + a_n², где a_t = dv/dt, a_n = v²/r. Следовательно, связь между полным линейным ускорением, тангенциальным и нормальным ускорениями имеет вид:

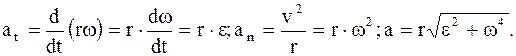(2.23)

Из написанных формул видно, что тангенциальное, нормальное и полное ускорения растут с увеличением расстояния от этих точек до оси вращения.

Можно показать, что любое сложное движение можно представить в виде поступательного и вращательного движений.

Надо отметить, что к вращательному движению применимы все формулы кинематики материальной точки, с заменой в них линейных величин соответствующими угловыми величинами. Например:

S = v₀t + at²/2; φ = ω₀t + εt² /2. (2.24)

Уравнением вращательного движения в кинематике называют выражение, которое отображает функциональную зависимость угла поворота от времени:

j = f(t).

В физике в качестве основной угловой меры принят радиан. Угол в радианах получается как отношение пройденного материальной точкой пути S к радиусу соответствующей окружности (см. рис.2.5):

.

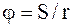2.5. Гармонические колебательные движения и их характеристики: смещение, амплитуда, период, частота, фаза,
скорость и ускорение

Колебания - движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания свойственны всем явлениям природы: пульсирует излучение звезд, внутри которых происходят циклические ядерные реакции; с высокой степенью периодичности вращаются планеты Солнечной системы; движение Луны вызывает приливы и отливы на Земле; в земной ионосфере и атмосфере циркулируют потоки заряженных и нейтральных частиц; ветры возбуждают колебания и волны на поверхности водоемов. Внутри любого живого организма непрерывно происходят разнообразные, ритмично повторяющиеся процессы. В виде сложнейшей совокупности колебаний частиц и полей (электронов, протонов, фотонов) можно представить "устройство" микромира.

В технике колебания либо выполняют определенные функциональные обязанности (маятник, колебательный контур, генератор), либо возникают как неизбежное проявление физических свойств (вибрация машин и сооружений, неустойчивости и вихревые потоки при движении тел в газах).

В физике выделяются механические, электромагнитные колебательные движения и их комбинации. Это обусловлено той исключительной ролью, которую играют гравитационные и электромагнитные взаимодействия в масштабах, характерных для жизнедеятельности человека. С помощью распространяющихся механических колебаний плотности и давления воздуха, воспринимаемых нами как звук, а также очень быстрых колебаний электрических и магнитных полей, воспринимаемых нами как свет, мы получаем прямую информацию об окружающем мире.

Колебания любых физических величин почти всегда связаны с попеременным превращением энергии одного вида в энергию другого вида.

По мере изучения колебаний различной физической природы возникло убеждение о возможности общего подхода к ним, основанного на свойствах и закономерностях колебательных процессов вообще. В результате появилась теория колебаний и волн. Одним из основных математических аппаратов теории колебаний являются дифференциальные уравнения.

При изучении колебательных движений обычно определяют закон, по которому повторяются движения, время, через которое система вновь возвращается в первоначальное состояние, наибольшее отклонение, которого достигает движущиеся материальная точка (тело). Установив эти характеристики колебательного движения, можно определить состояние системы в любой момент времени.

Все сложные виды колебательных движений можно свести к простейшему виду - гармоническим колебаниям.

Гармоническими колебаниями называют такие периодически повторяющиеся движения материальной точки (тела), при которых ее смещение от положения равновесия изменяется по закону синуса или косинуса:

(2.25)

где x – смещение. Удаление материальной точки от положения равновесия в данный момент времени t;

x₀- амплитуда колебаний. Наибольшее (максимальное) удаление материальной точки от положения равновесия;

(wt + j₀) - фаза колебаний. Определяет положение материальной точки в данный момент времени t. Это периодически изменяющийся аргумент функции, описывающей колебательный или волновой процесс.

j₀ - начальная фаза колебаний. Определяет положение материальной точки в начальный момент времени t = 0;

w = 2p/T = 2pn - круговая (циклическая) частота колебаний. Определяет число колебаний, совершаемых за время, t = 2p;

T - период колебаний. Время, за которое совершается одно полное колебание;

n - частота колебаний. Число колебаний, совершаемых в единицу времени.

Скорость материальной точки, совершающей гармоническое колебательное движение, - физическая величина, которая показывает, как изменяется смещение в единицу времени, численно равная первой производной от смещения по времени:

(2.26)

Ускорение материальной точки, совершающей гармоническое колебание, - физическая величина, которая показывает, как изменяется скорость материальной точки в единицу времени, численно равная первой производной от скорости или второй производной от смещения по времени:

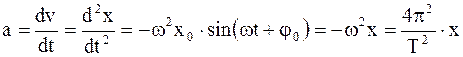. (2.27)

Знак "минус" означает, что ускорение направлено в сторону, противоположную смещению.

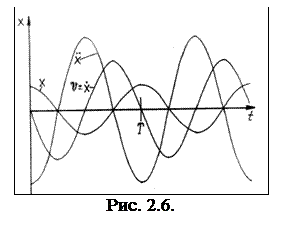
Из соотношений видно, что скорость имеет максимальное значение, когда точка проходит положение равновесия, а ускорение в крайних положениях.

Изменение смещения, скорости и ускорения с течением времени при гармонических колебательных движениях представлено на рис. 2.6

2.6. Методы сложения гармонических колебаний. Векторные
диаграммы. Сложение гармонических колебаний одного
направления и одинаковой частоты. Биения

Колебания, совершаемые материальными точками, телами, системами, чаще всего являются результатом сложения нескольких гармонических колебаний, совершаемых одновременно. Следовательно, любое сложное колебание можно разложить на несколько простых (гармонических). Для того чтобы знать, как зависит характер сложного колебания от соотношения фаз, частот, амплитуд и направлений складываемых колебаний, рассмотрим наиболее простые случаи сложения гармонических колебаний. Основными методами сложения колебаний являются метод векторных диаграмм и аналитический метод.

Метод векторных диаграмм заключается в том, что гармонические колебания изображаются графически в виде вектора на плоскости. Для этого из начала координат на плоскости проводят вектор, модуль которого равен амплитуде рассматриваемых колебаний, который составляет с осью координат (горизонтальной осью) угол j = wt + j₀, равный фазе колебаний в данный момент времени t (рис.2.7).

С течением времени угол j увеличивается так, что вектор равномерно вращается относительно начала координат с угловой скоростью, равной циклической частоте w. Соответственно проекция вектора на вертикальную ось совершает гармонические колебания по закону:

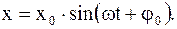(2.28)

Этим методом широко пользуются при сложении одинаково направленных гармонических колебаний.

Предположим, что имеются два гармонических колебания с одинаковой частотой w₁ = w₂ = w (T₁ = T₂ = T), но с разными амплитудами x₀₁ ¹ x₀₂ и начальными фазами j₀₁ ¹ j₀₂. Уравнения таких колебаний будут иметь вид:

x₁ = x₀₁×sin(wt + j₀₁); x₂ = x₀₂×sin(wt + j₀₂). (2.29)

Изобразив эти колебания в виде векторной диаграммы, для амплитуды результирующего колебания получим:

x₀ = x₀₁ + x₀₂. (2.30)

Численное значение амплитуды результирующего колебания можно определить по теореме косинусов:

x₀² = x₀₁² + x₀₂² - 2x₀₁×x₀₂×cos[p - (j₁ - j₂)] =

= x₀₁² + x₀₂² - 2x₀₁×x₀₂×cos(j₁ - j₂)]. (2.31)

Пользуясь векторной диаграммой, определяем начальную фазу результирующего колебания:

(2.32)

Уравнение результирующего колебания будет иметь вид

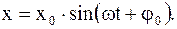(2.33)

Анализ полученного результата приводит к следующим выводам:

1. При j₀₁ - j₀₂ = 2pk - разность начальных фаз складываемых колебаний равна четному числу p; в частности при k = 0, (j₀₁ - j₀₂ = 0):

x₀ = x₀₁ + x₀₂; tgj₀ = tgj₀₁ = tgj₀₂; j₀ = j₀₁ = j₀₂. (2.34)

Колебания синфазные и усиливают друг друга.

2. При j₀₁ - j₀₂ = (2k + 1)p - разность начальных фаз складываемых колебаний равна нечетному числу p; в частности при k = 0, (j₀₁ - j₀₂) = p:

x₀ = x₀₁ – x₀₂; j₀₁ = -j₀₂. (2.35)

Колебания противофазные и ослабляют друг друга.

3. При x₀₁ = x₀₂; w₁ = w₂ = w; j₀₂ ¹ j₀₁. Уравнения таких гармонических колебаний имеют вид

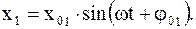(2.36)

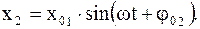(2.37)

Для получения уравнения результирующего колебания воспользуемся аналитическим методом сложения колебаний. В этом случае будем иметь

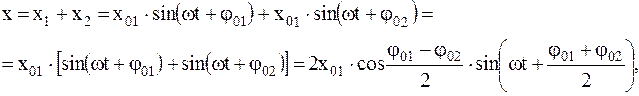
(2.38)

где 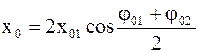- амплитуда результирующего колебания;

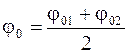- фаза результирующего колебания.

Результирующее колебание - гармоническое, такой же частоты, отличающееся по фазе от складываемых колебаний на половину суммы их начальных фаз.

Из полученного результата видно, что:

а) при j₀₁ - j₀₂ = 2kp - разность начальных фаз складываемых колебаний равна четному числу p; в частности при k = 0 (j₀₁ - j₀₂ = 0):

x₀ = 2x₀₁. (2.39)

Колебания усиливают друг друга;

б) при j₀₁ - j₀₂ = (2k + 1)p - разность начальных фаз складываемых колебаний равна нечетному числу p; в частности при k=0 (j₀₁ - j₀₂ = p):

x₀ = x₀₂ – x₀₁ = 0. (2.40)

Колебания гасят друг друга. В остальных случаях амплитуда результирующего колебания меньше суммы амплитуд складываемых колебаний.

Особый интерес представляет сложение колебаний одного направления, амплитуды которых одинаковы (x₀₂ = x₀₁); начальные фазы равны 0 (j₀₁=j₀₂=0), а круговые частоты мало отличаются друг от друга (w₁» w₂). Уравнения таких колебаний имеют вид

x₁ = x₀₁×sinw₁t; x₂ = x₀₁×sinw₂t. (2.41)

Уравнение результирующего колебания запишем, если воспользуемся аналитическим методом сложения гармонических колебаний:

x = x₁ + x₂ = x₀₁×sinw₁t + x₀₁×sinw₂t = 2x₀₁×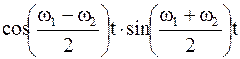, (2.42)

где 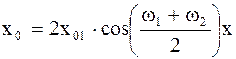- амплитуда результирующего колебания, которая зависит от Dw = w₁ - w₂ – разности частот складываемых колебаний.

- смещение результирующего колебания, изменяющееся по гармоническому закону.

Так как 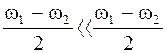, то амплитуда результирующего колебания изменяется со временем медленнее, чем смещение. Поэтому результирующее колебание можно считать почти гармоническим. Частота и период результирующего колебания соответственно будут равны

(2.43)

Частота и период изменения амплитуды (частота и период биения):

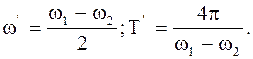(2.44)

Такие колебания называются биениями.

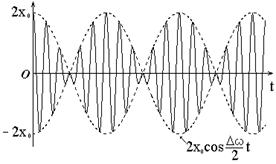Рис.2.8

Процесс возникновения и характер биений можно представить так (рис.2.8): в начале (при t = 0) фазы складываемых колебаний совпадают, амплитуда результирующего колебания максимальна. По мере нарастания разности фаз амплитуда результирующего колебания уменьшается, становится меньше суммы амплитуд складываемых колебаний. При разности фаз, равной p, складываемые колебания погасят друг друга (x₀ = 0). Дальнейшее увеличение разности фаз приведет к возрастанию амплитуды результирующего колебания, и при разности фаз, равной 2p, достигнет вновь максимального значения, затем процесс будет повторяться.

Периодическое изменение амплитуды от до 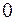обусловлено постепенным запаздыванием по фазе одного из исходных колебаний: при разности фаз исходных колебаний, равной (где 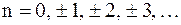), амплитуда результирующего колебания равна , а при разности фаз, равной 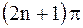(где 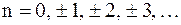), амплитуда равна .

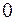Одним из применений получения биений является настройка музыкальных инструментов. Настройщик рояля, например, добивается "нулевых" биений звуковых колебаний от эталонных камертонов и струн музыкального инструмента (постепенно натягивая или отпуская струну, он добивается максимального снижения частоты результирующего звукового колебания, благодаря чему процесс настройки становится стандартным и очень точным). В так называемых "гетеродинных" частотомерах также используется принцип нулевых биений для идентификации частоты нового источника колебаний.

В результате сложения гармонических колебаний, совпадающих по направлению и имеющих кратные циклические частоты w, 2w, 3w и т.д., получаются периодические негармонические колебания с периодом T = 2p/w. В свою очередь, любое сложное периодическое колебание x = f(t) можно представить в виде суммы простых гармонических колебаний с циклическими частотами, кратными основной циклической частоте w = 2p/T, где T - период колебаний:

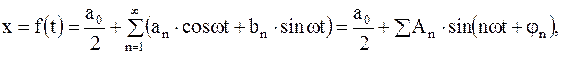(2.45)

где , при (n = 0, 1, 2, …..);

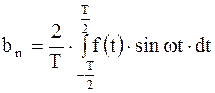, при (n = 1, 2, …..).

Такое представление периодической функции f(t) называется разложением этой функции в ряд Фурье или гармоническим анализом сложного периодического колебания. Члены ряда Фурье, соответствующие гармоническим колебаниям с циклическими частотами w, 2w, 3w и т.д., называются первой, или основной, второй, третьей и т.д. гармониками сложного периодического колебания x = f(t). Совокупность этих гармоник образует спектр колебания x = f(t). Состав спектра зависит от вида периодической функции x = f(t). В простейших случаях спектр может состоять из небольшого числа гармоник.

Часто под спектром колебания понимают спектр его частот, т.е. совокупность частот простых гармонических колебаний, в результате сложения которых может быть получено рассматриваемое сложное колебание. Периодические колебания имеют дискретные (линейчатые) спектры частот.

2.7. Сложение взаимно перпендикулярных колебаний.
Фигуры Лиссажу

Рассмотрим движение материальной точки, участвующей одновременно в двух взаимно перпендикулярных колебаниях, частоты которых w₁ и w₂ равны

(w₁ =w₂=w), в направлениях осей "x" и "y".

В этом случае колебательный процесс описывается следующей системой уравнений:

x = x₀×sinwt, y = y₀×cos(wt + j). (2.46)

Для определения уравнения траектории движения точки из системы уравнений исключим время. Из первого уравнения имеем

x/x₀ = sinwt. (2.47)

Второе уравнение системы перепишем в виде

y = y₀×cos(wt + j) = y₀×(sinwt×cosj + coswt×sinj), (2.48)

но

coswt = [1 – sin²wt]^1/2 = [1 - (x/x₀)²]^1/2. (2.49)

Подставив вместо sinwt и coswt их значения, получим уравнение траектории движения материальной точки:

y = y₀{(x/x₀)×cosj + [1 - (x/x₀)²]^1/2×sinj}, (2.50)

или

y = (y₀/x₀)×{x×cosj + [x₀² – x²]^1/2×sinj}. (2.51)

Исследуем некоторые частные случаи.

1. Складываемые колебания имеют одинаковые частоты (w₁ = w₂ =w), различные амплитуды (x₀ ¹ y₀) и начальные фазы j₁ = j₂ = 0, уравнения которых имеют вид

x = x₀×sinwt, y = y₀×sinwt. (2.52)

Уравнение траектории движения точки в этом случае:

y = (y₀/x₀)×x. (2.53)

Уравнение (2.53) является уравнением прямой, проходящей через начало координат, наклон которой к оси x определяется углом a: tga = y₀/x₀. Смещение материальной точки от начала координат
r² = (x₀² + y₀²)×sin²wt.

Результирующее колебание является гармоническим.

2. Складываемые колебания имеют одинаковые частоты
(w₁ =w₂ = w), различные амплитуды (x₀ ¹ y₀), начальные фазы j₁ и j₂, отличающиеся на p/2.

Уравнение траектории в этом случае имеет следующий вид:

y = y₀×[1 - (x/x₀)²]^1/2 или (y/y₀)² + (x/x₀)² = 1. (2.54)

Следовательно, в данном случае траектория результирующего движения представляет собой эллипс с полуосями, равными x₀ и y₀.

Рис.2.9

При равных амплитудах (x₀ = y₀) траектория результирующего движения - окружность. Некоторые из рассмотренных случаев сложения взаимно перпендикулярных колебаний представлены на рис.2.9.

В общих случаях сложения взаимно перпендикулярных гармонических колебаний замкнутые траектории точки называются фигурами Лиссажу. Конфигурация этих кривых зависит от соотношения амплитуд, начальных фаз, периодов и частот складываемых колебаний (рис.2.10).

    Рис.2.10

Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, соответственно равных амплитудам складываемых колебаний. Отношение частот складываемых колебаний равно отношению числа касаний соответствующей им фигуры Лиссажу со сторонами прямоугольника, параллельными осям.

Сложение колебаний, направленных под прямым углом друг к другу, достаточно часто происходит в различных процессах, протекающих в природе и в различных технических устройствах. Например, при подаче переменного напряжения на две пары отклоняющих пластин электронно-лучевой трубки электронный пучок одновременно участвует в двух взаимно перпендикулярных колебаниях. На экране электронно-лучевой трубки можно наблюдать траекторию результирующего колебательного движения (фигуры Лиссажу).

Дата добавления: 2014-01-06