Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета

Силы инерции при ускоренном движении системы отсчета

Описание движения в неинерциальных системах отсчета

С учетом сил инерции второй закон Ньютона будет справедлив для любых систем: произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (включая и силы инерции). Силы инерции F _ин при этом должны быть такими, чтобы вместе с силами F, обусловленными воздействием тел друг на друга, они сообщали телу ускорение a ^’, каким оно обладает в неинерциальных системах отсчета, т.е.

m a ^’= F + F _ин. (3.20)

Так как F = m a (a - ускорение тела в инерциальной системе отсчета), то

m a ^’=m a + F _ин. (3.21)

Силы инерции обусловлены ускоренным движением системы отсчета относительно выбранной системы, поэтому необходимо учитывать проявления этих сил в следующих случаях: 1) при ускоренном (замедленном) поступательном движении системы отсчета; 2) когда они действуют на покоящееся тело во вращающейся системе отсчета; 3) когда они действуют на тело, движущееся во вращающейся системе отсчета.

Рассмотрим движение шарика, подвешенного на штативе, расположенном на легко подвижной тележке. Пока тележка находится в покое или движется равномерно и прямолинейно, нить, удерживающая шарик, занимает вертикальное положение, и сила тяжести P уравновешивается реакцией нити T.

Если заставить тележку двигаться поступательно с некоторым ускорением

a ₀, то нить начнет отклоняться от вертикали в сторону противоположную движению тележки до такого угла a, пока результирующая сила F = P + T не сообщит шарику ускорение, равное a ₀. (рис. 3.2). Таким образом, результирующая сила F направлена по направлению ускорения a ₀. Для установившегося движения шарика, который теперь движется с данным ускорением, результирующая сила

F = mg×tga = m×a₀, (3.22)

откуда угол отклонения нити от вертикали

tgα = a₀/g, (3.23)

т.е. зависит от ускорения a₀; чем оно больше, тем угол α больше.

Относительно системы отсчета, связанной с движущейся тележкой, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной силой F _ин, которая и является силой инерции, так как на шарик никакие другие силы не действуют. Таким образом

F _ин = - m a ₀. (3.24)

Проявление сил инерции наблюдается в повседневных явлениях, например, они возникают при запуске и торможении космических аппаратов, вызывая значительные перегрузки.

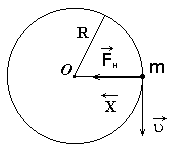
    Рис.3.3

К неинерциальным системам отсчета часто прибегают при рассмотрении вопросов вращательного движения. Хорошо известно явление, когда на больших оборотах разваливается на куски массивный маховик. Говорят, что он разрушился под действием "центробежных сил". Понятие центробежной силы применимо лишь к неинерциальной системе отсчета, жестко связанной с вращающимся телом.

Рассмотрим простой пример вращения шарика, удерживаемого нитью, вокруг точки О (рис.3.3). В инерциальной системе отсчета на шарик действует сила натяжения нити. Уравнение движения в этой системе отсчета имеет вид

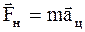или . (3.25)

В неинерциальной системе отсчета действуют сила натяжения нити и центробежная сила инерции. Уравнение движения в такой системе запишется так:

или 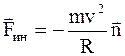, (3.26)

где – единичный вектор, направленный к центру вдоль радиуса.

Аналогично для некоторого диска, на котором к штативу подвешен шарик массой m. Диск может равномерно вращаться с некоторой угловой скоростью w. В инерциальной системе отсчета, связанной, например, с помещением, где находится диск, шарик равномерно вращается по окружности радиусом R (расстояние от точки подвеса шарика к диску до оси вращения), отклонившись от вертикального положения. Следовательно, на шарик действует сила, равная F = mw²×R и направленная перпендикулярно оси вращения диска. Она является равнодействующей силы тяжести P и силы натяжения нити T:

F = P + T. (3.27)

Когда движение шарика установившееся, то

F = mg×tga = mw²×R, (3.28)

откуда

tgα = ω²R/g. (3.29)

Таким образом, угол отклонения нити, на которой подвешен шарик, будет тем больше, чем больше расстояние R от шарика до оси вращения диска и чем больше угловая скорость вращения ω.

Относительно системы отсчета, связанной с вращающимся диском, шарик покоится, что возможно, когда сила F уравновешивается равной по величине и противоположной по направлению силой, которая и является силой инерции F _ц. Эта сила называется центробежной силой инерции. Она направлена по горизонтали в сторону от оси вращения и определяется по формуле (рис. 3.4)

F_ц = - mω²×R. (3.30)

Действие центробежных сил инерции проявляется в различных физических явлениях. Они широко используются во всех центробежных механизмах, где достигают больших значений. При проектировании быстро вращающихся деталей машин и механизмов принимают меры для компенсации центробежных сил инерции.

Центробежная сила инерции, действующая на тела во вращающихся системах отсчета в направлении от оси вращения, не зависит от скорости тел относительно вращающихся систем отсчета. Следовательно, центробежная сила инерции действует во вращающихся системах отсчета на все тела, удаленные от оси вращения на конечное расстояние, независимо от того, покоятся ли они в этой системе отсчета или движутся относительно нее с какой-то скоростью.

3.3.3. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета (сила Кориолиса)

При движении тела относительно вращающейся системы отсчета, кроме центробежной силы инерции, появляется еще одна сила, называемая силой Кориолиса или кориолисовой силой инерции. Рассмотрим проявление этой силы на одном частном примере.

Рис.3.5

Относительно вращающейся системы отсчета тело движется по окружности, лежащей в плоскости, перпендикулярной к оси вращения, причем центр окружности лежит на этой оси. Такой случай реализуется, например, когда тело движется вдоль параллели (экватора) по поверхности вращающегося земного шара (рис.3.5).

Относительно неподвижной (инерциальной) системы тело движется равномерно по окружности радиуса R. Так что ускорение тела в этой системе (центростремительное) может быть представлено в виде

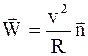, (3.31)

где .

После выполнения простых преобразований получим

или . (3.32)

По отношению к вращающейся системе тело обладает центростремительным ускорением

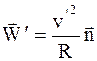. (3.33)

Откуда следует, что первое слагаемое в (3.32) представляет собой ускорение 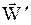. Следовательно,

. (3.34)

В соответствии с этим выражением сила инерции оказывается состоящей из двух компонент:

. (3.35)

Первая из них есть центробежная сила инерции , вторая – кориолисова сила . Сила имеет направление:

а) от центра, если скорости v^’ и wR совпадают по направлению;

б) к центру, если скорости v¢ и wR направлены в противоположные стороны.

В общем случае, когда вектор скорости v материальной точки, перемещающейся по вращающейся поверхности, направлен произвольно, математическое выражение силы Кориолиса таково:

. (3.36)

Вектор F _к перпендикулярен векторам скорости v ^’ тела и угловой скорости вращения ω системы отсчета в соответствии с правилом правого винта.

В таблице 3.1 наглядно показаны силы инерции, возникающие в зависимости от состояния частицы в неинерциальной системе отсчета и характера движения этой системы относительно инерциальной системы отсчета.

Таблица 3.1

Дата добавления: 2014-01-06