Лекция 4. Физика колебаний. Гармонический осциллятор. Нормальные моды

Дифференциальное уравнение гармонических колебаний и его решение. Модель гармонического осциллятора. Примеры гармонических осцилляторов: физический, математический и пружинный маятники. Определение их периодов и частот. Свободные колебания. Дифференциальное уравнение затухающих колебаний и его решение. Характеристики затухающих колебаний: коэффициент затухания, декремент, логарифмический декремент затухания, добротность. Вынужденные колебания гармонического осциллятора под действием синусоидальной силы. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний. Резонанс. Параметрический резонанс.

4.1. Дифференциальное уравнение гармонических колебаний и его решение

Воспользовавшись основным уравнением классической динамики (уравнением второго закона Ньютона) можно получить уравнение движения материальной точки (тела), совершающего гармоническое колебание:

F = m a или F = ma, (4.1)

где a = d²x/dt² = - ω₀² x - ускорение материальной точки;

F = å F _i- результирующая сила, под действием которой совершается гармоническое колебание (возвращающая сила);

F _i - i-я сила, действующая на материальную точку.

Тогда

F = - mω₀²x = - kx, (4.2)

где k = mω₀² - коэффициент возвращающей силы, физический смысл которого заключается в том, что он численно равен возвращающей силе, вызывающей единичное смещение.

Из уравнения (4.2) видно, что сила, под действием которой совершается гармоническое колебание, пропорциональна смещению и направлена в сторону противоположную ему. Она называется возвращающей силой. Возвращающая сила стремится вернуть материальную точку в положение равновесия.

Возвращающие силы могут иметь различную природу. Например, они могут возникать за счет деформации. Силы, возникающие за счет упругой деформации, называются упругими. Силы, имеющие иную природу, - квазиупругими (как бы упругими).

Таким образом, уравнение движения материальной точки при гармоническом колебательном движении имеет вид

или 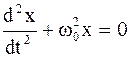. (4.3)

С точки зрения математики уравнение (4.3) - однородное дифференциальное второго порядка, решением которого является выражение вида

x = x₀×sin(ω₀t + φ₀), (4.4)

где x - смещение;

x₀ - амплитуда;

ω₀ - собственная (круговая или циклическая) частота;

φ₀ - начальная фаза.

Решая дифференциальное уравнение гармонического колебательного движения, можно получить значение, например, периода колебаний, собственной частоты.

4.2. Примеры гармонических осцилляторов. Физический, математический и пружинный маятники.
Определение их периодов и частот

Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида (4.3):

или .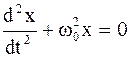

Колебания гармонического осциллятора являются примером периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики.

В качестве примеров гармонических осцилляторов рассмотрим гармонические колебания систем, называемых пружинным, физическим и математическим маятниками.

Дата добавления: 2014-01-06