Лекция 5. Ангармонические колебания

Нелинейный осциллятор. Физические системы, содержащие нелинейность. Автоколебания. Условие самовозбуждения колебаний. Роль нелинейности. Предельные циклы.

5.1. Нелинейный осциллятор. Физические системы,
содержащие нелинейность

Известно, что осциллятор - физическая система, совершающая колебания. Термином "осциллятор" пользуются для любой системы, если описывающие ее величины периодически меняются со временем.

Классический осциллятор - механическая система, совершающая колебания около положения устойчивого равновесия (например, маятник, груз на пружине). В положении равновесия потенциальная энергия U системы имеет минимум. Если отклонения x от этого положения малы, то в разложении U(x) по степеням x можно принять

, (5.1)

где k - постоянный коэффициент.

При этом квазиупругая сила

F = -dU/dx = - kx. (5.2)

Такие осцилляторы называются гармоническими, их движение описывается линейным уравнением

, (5.3)

решение которого имеет вид

x = A sin (wt + j), (5.4)

где m - масса осциллятора;

A - амплитуда колебаний;

w = 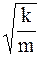- циклическая частота;

j - начальная фаза колебаний;

t - время.

Полная энергия гармонического осциллятора

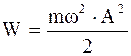(5.5)

является суммой периодически меняющихся в противофазе кинетической (Т) и потенциальной (U) энергий, независящей от времени:

W = T + U. (5.6)

Когда отклонение x нельзя считать малым, в разложении U(x) необходим учет членов более высокого порядка - уравнения движения становятся нелинейными, т. е. такими, в которых переменные и их производные входят в высших степенях, например - в третьей степени. Это внесло математические затруднения в решении этих и подобных им проблем.

Примером такого уравнения может служить уравнение генератора электромагнитных волн

, (5.7)

которое содержит третью степень производной от y.

Голландский физик Ван дер Поль в ряде работ (с 1920 г.) дал приближенные решения некоторых нелинейных уравнений и тем самым положил начало изучению нелинейных колебаний.

Большой вклад в развитие теории нелинейных колебаний внес А.А. Андронов (1901 -1952), академик, профессор Горьковского университета.

Осцилляторы, удовлетворяющие нелинейным уравнениям, называют нелинейными или ангармоническими.

Понятие осциллятор применяется также к немеханическим колебательным системам. В частности, колебательный контур является электрическим осциллятором. Колебания напряженностей электрического и магнитного полей в плоской электромагнитной волне также можно описывать с помощью понятия осциллятор.

В квантовой механике задача о линейном (с одной степенью свободы) гармоническом осцилляторе решается с помощью уравнения Шредингера (с U= kx²/2). Решение существует лишь для дискретного набора значений энергии

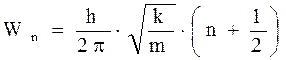, (5.8)

где n = 1, 2,...

Важной особенностью энергетического спектра осциллятора является то, что уровни энергии W_n расположены на равных расстояниях. Так как правила отбора разрешают в данном случае переходы только между соседними уровнями, то (хотя квантовый осциллятор имеет набор собственных частот w_n = 2p∙W_n/h) излучение его происходит на одной частоте w, совпадающей с классической w = (k/m)^1/2. В отличие от классического осциллятора возможное наименьшее значение энергии (при n = 0) квантового осциллятора равно не нулю, а hw/4p (нулевая энергия).

Понятие осциллятор играет важную роль в теории твердого тела, электромагнитного излучения, колебательных спектров молекул.

Нелинейные системы - колебательные системы, свойства которых зависят от происходящих в них процессов.

Нелинейными являются: механические системы, в которых модули упругости тел зависят от деформаций последних или коэффициент трения между поверхностями тел зависит от относительной скорости этих тел (скорости скольжения); электрические системы, содержащие сегнетоэлектрики, диэлектрическая проницаемость которых зависит от напряженности электрического поля.

Указанные зависимости в механических системах приводят соответственно либо к нелинейности связей между напряжениями и деформациями (нарушению закона Гука), либо к нелинейной зависимости сил трения от скорости скольжения, либо к нелинейной связи между действующей на тело силой и сообщаемым ему ускорением (если при этом скорость тела меняется по величине). Каждая из этих нелинейных связей приводит к тому, что дифференциальные уравнения, описывающие поведение нелинейных систем, оказываются нелинейными. Поэтому и системы называются нелинейными.

Все физические системы являются нелинейными. Поведение нелинейных систем существенно отличается от поведения линейных систем. Одна из наиболее характерных особенностей нелинейных систем - нарушение в них принципа суперпозиции.

5.2. Автоколебания. Обратная связь. Условие самовозбуждения. Роль нелинейности. Предельные циклы

Автоколебаниями называются вынужденные незатухающие колебания в реальных системах, период и амплитуда которых не зависят от характера внешнего воздействия, а определяются свойствами самой автоколебательной системы.

Автоколебания поддерживаются за счет энергии от внешнего источника, причем количество поступающей энергии регулируется самой системой. В отличие от незатухающих собственных колебаний гармонического осциллятора и аналогичных систем, амплитуды которых определяются начальными условиями, амплитуды которых определяются начальными условиями, амплитуды автоколебаний от начальных условий не зависят.

Собственные незатухающие колебания относятся к идеализированному типу колебаний, который в реальных системах никогда не реализуется точно. Реальные собственные колебания всегда затухают. Напротив, автоколебания в реальных системах могут продолжаться сколь угодно долго, пока не израсходуется энергия источника, поддерживающая эти колебания.

Примеров автоколебательных систем довольно много. Автоколебания могут возбуждаться и поддерживаться также периодическими силами. Однако период последних не имеет никакого отношения к периоду возбуждаемых автоколебаний.

Строгая теория автоколебаний весьма сложна. Это связано с тем, что автоколебания нелинейны, т. е. описываются нелинейными уравнениями. Принцип суперпозиции в этих случаях не выполняется, что затрудняет получение и исследование решений самих уравнений.

Дата добавления: 2014-01-06