Пружинный маятник

Пружинный маятник - тело массой m, подвешенное на абсолютно упругой пружине, совершающее гармоническое колебание.

Рассмотрим простую колебательную систему: верхний конец пружины зафиксирован, а нижний соединён с некоторым телом, имеющим массу 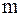(рис.4.1). При растяжении пружины тело смещается из положения равновесия. Пружина характеризуется коэффициентом жесткости 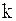. Мы рассматриваем колебательную систему с сосредоточенными параметрам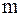и и 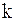, т.е. мы считаем, что масса сосредоточена в присоединённом теле, а упругость (жёсткость) характерна исключительно для пружины. На самом деле такое допущение – очередная абстракция, т.к. любая пружина имеет конечную (не нулевую) массу, а любое физическое тело обладает некоторой упругостью.

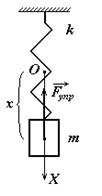Рис.4.1

В действительности мы можем говорить лишь о преимущественном распределении параметров 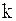и 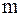соответственно в пружине и в присоединённом к ней теле.

Направим вертикально вниз ось 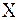, причем начало оси совместим с положением равновесия тела. При смещении тела из положения равновесия на него действует сила упругости 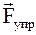. То есть в этом случае колебания возникают под действием сил упругой деформации F (возвращающей, упругой силы), пропорциональной деформации Dl = x.

В данном случае действие силы тяжести не учитывается, т.к. оно приводит лишь к некоторому смещению тела из положения равновесия (точнее, к смещению самого положения равновесия) и никак не влияет на колебательный процесс. Беря проекцию силы упругости на ось , запишем:

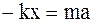или . (4.5)

Разделив на обе части дифференциального уравнения и введя обозначение 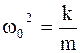, перепишем уравнение в следующем виде:

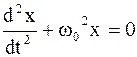. (4.6)

Решением дифференциального уравнения (4.6) является функция 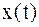, подстановка которой обращает уравнение в тождество. В данном случае решением является функция

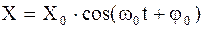. (4.7)

В чем нетрудно убедиться, осуществив подстановку:

, ;

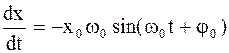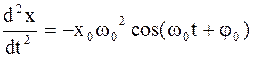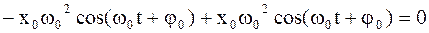. (4.8)

Параметр 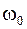называется собственной частотой свободных незатухающих колебаний. Таким образом, выведенная из равновесия система совершает незатухающие гармонические колебания с вполне определённой для неё частотой .

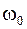Решая дифференциальное уравнение, можно получить выражения для собственной частоты и периода колебаний пружинного маятника. Для чего в дифференциальное уравнение (уравнение движения пружинного маятника) необходимо подставить значения x = x₀×sin(ω₀t + φ₀) и d²x/dt² = - ω₀²x. Будем иметь

- mω₀²x + kx = 0; - mω₀² + k = 0, (4.7)

откуда

. (4.9)

Так как T = 2π/ω₀, то для периода колебаний пружинного маятника получим

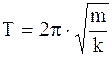. (4.10)

Надо отметить, что приведенное справедливо для упругих колебаний в пределах, в которых выполняется закон Гука, т.е. когда масса пружины мала по сравнению с массой тела.

Анализируя колебательный процесс, мы приходим к выводу, что признаками колебательной системы являются следующие три:

1) положение равновесия, 2) возвращающая сила, 3) инерция.

Дата добавления: 2014-01-06