Физический и математический маятники

Физический маятник - твердое тело, способное совершать гармоническое колебательное движение относительно оси, на которой оно подвешено. При этом ось не проходит через центр тяжести (рис.4.2).

В поле сил тяготения колебания физического маятника происходят под действие возвращающей силы, составляющей силы тяготения F _т = m g, которую можно разложить на две составляющие: по направлению прямой, перпендикулярной осиF_n, и по направлению, перпендикулярному данному – F_τ. Составляющая F_n не создают вращающего момента, так как она перпендикулярна оси вращения (колебания). Поэтому возвращающей силой, создающей вращающий момент в данном случае, является

F_τ = - mg×sinj, (4.11)

где j - угол отклонения физического маятника от положения равновесия.

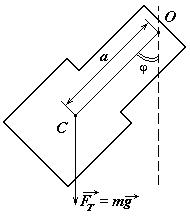Рис.4.2  

При малых углах отклонения (j®0) sinj®j, следовательно,
F_τ= - mg×j, а момент этой силы

M = - mgj×a, (4.12)

где a - расстояние от точки приложения силы до оси вращения.

Согласно основному уравнению динамики вращательного движения этот вращающий момент M численно равен I×ε:

M = I∙ε. (4.13)

Таким образом, имеем

Iε == - mgja; Iε += - mgja = 0; 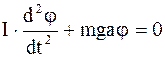. (4.14)

Полученное соотношение является уравнением движения физического маятника. С точки зрения математики, оно однородное, дифференциальное, второго порядка, решение которого имеет вид

j = j₀×sin(ω₀t + α), (4.15)

где α - начальная фаза колебаний.

Решая дифференциальное уравнение, можно определить круговую (циклическую) частоту и период колебаний физического маятника.

Так, подставив значение d²φ/dt² = - ω₀²φ в уравнение движения, будем иметь

-Iω₀²φ + mgaφ = 0; -Iω₀² + mga = 0. (4.16)

Откуда:

1) круговая или циклическая частота

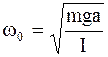; ; (4.17)

2) период колебаний

. (4.18)

Из полученных результатов видно, что при малых углах отклонения от положения равновесия физический маятник совершает гармонические колебания с соответствующими циклической частотой и периодом.

Одной из характеристик физического маятника является так называемая приведенная длина L_пр = I/ma, с учетом которой для циклической частоты и периода колебаний физического маятника, соответственно, можно записать

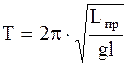;. (4.19)

Точка, расположенная на продолжении прямой, соединяющей ось подвеса с центром масс, находящаяся на расстоянии, равном приведенной длине L_пр, называется центом качаний физического маятника.

Используя теорему Штейнера, можно показать, что расстояние между осью подвеса и центром масс всегда меньше приведенной длины физического маятника:

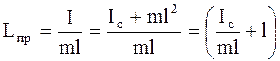>l. (4.20)

Рис.4.3  

Точка подвеса и центр качаний обладают свойством взаимозаменяемости: если ось подвеса перенести в центр качаний, то точка подвеса станет новым центром качаний, а период колебаний физического маятника не изменится.

Математический маятник - тело массой m, подвешенное на невесомой, нерастяжимой нити, размерами которого можно пренебречь (рис.4.3).

Математический маятник совершает гармонические колебания под действием силы тяжести, подобно физическому маятнику.

В этом случае математический маятник можно рассматривать как материальную точку, для которой момент инерции

I = m∙l², (4.21)

где l - длина математического маятника.

Так как математический маятник - частный случай физического маятника, вся масса которого сосредоточена в одной точке - центре масс, то, подставив в (4.19) значение (4.21) для циклической частоты и периода колебаний математического маятника, получим

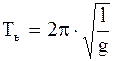;. (4.22)

Из (4.22) видно, что циклическая частота и период колебаний математического маятника зависит от его длины и ускорения свободного падения в данном месте пространства.

Сравнив формулы для определения циклических частот и периодов колебаний физического и математического маятников, можно установить физический смысл приведенной длины физического маятника: приведенная длина физического маятника - это физическая величина, численно равная длине такого математического маятника, период колебаний которого равен периоду колебаний физического маятника.

Надо отметить, что все рассмотренное справедливо для малых углов отклонения соответствующей системы от положения равновесия. Если данное условие не выполняется, то определение циклических частот и периодов колебаний представляется довольно трудной задачей, так как в этом случае они функционально оказываются зависимыми от угла отклонения:

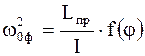;; (4.23)

;. (4.24)

4.3. Свободные (затухающие колебания). Дифференциальное уравнение затухающих колебаний и его решение.
Характеристики затухающих колебаний

Колебательные движения реальной колебательной системы всегда сопровождаются силами трения и сопротивления, которые приводят к уменьшению амплитуды колебаний. Если энергия, потерянная системой, не восполняется за счет внешних сил, то колебания системы называются затухающими, свободными или собственными.

В линейных системах свободные колебания представляют собой суперпозицию нормальных колебаний (нормальных мод).

    Рис.4.4

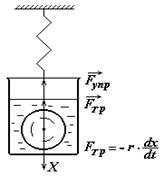
Cделаем существенное приближение к действительности, если учтем наличие силы сопротивления (трения) 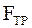, т.е. учтем диссипадию энергии колебательной системы. Предположим, что сила трения обусловлена внутренним трением в результате движения тела в вязкой среде (рис.4.4).

Ограничившись, случаем малых колебаний, воспользовавшись основным законом динамики, можно записать уравнение затухающих колебаний.

На систему в этом случае действуют две силы: возвращающая F₁ и силасопротивления F₂, которая при малых скоростях движения v пропорциональна скорости:

F₁ = - kx; (4.25)

F₂ = - rv = - r×dx/dt, (4.26)

где r - коэффициент сопротивления.

Таким образом, уравнение затухающих колебаний будет иметь вид

m a = F ₁+ F ₂; ma = F₁ + F₂.;

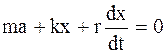
или окончательно

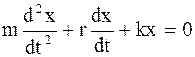. (4.27)

Этому дифференциальному уравнению (второго порядка) затухающих колебаний соответствует решение

, (4.28)

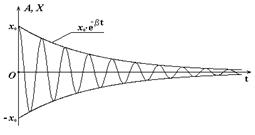
где А = x₀×e^-βt - амплитуда колебаний, которая убывает по экспоненциальному закону;

β = r/(2m) или - коэффициент затухания, характеризующий быстроту убывания амплитуды с течением времени.;

t - время, в течение которого амплитуда колебаний убывает в два раза;

ω₀² = k/m – собственная частота колебаний системы, т.е. та частота, совершались бы свободные колебания системы в отсутствии сопротивления среды (r = 0).

Решая дифференциальное уравнение, можно определить частоту и период затухающих колебаний:

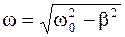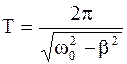; . (4.29)

Отметим, что на практике 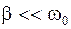, поэтому можно считать .

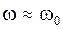Так как

    Рис.4.5

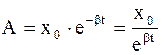, (4.30)

то действительно при t®¥, A®0.

Графически затухающие колебания можно представить так, как показано на рис.4.5.

Основными характеристиками затухающих колебаний являются декремент и логарифмический декремент затухания.

Декремент затухания - отношение двух смещений, отличающихся друг от друга по времени на период

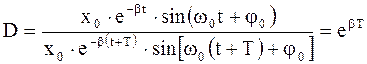. (4.31)

Декремент затухания характеризует быстроту затухания в зависимости от числа колебаний. По его величине можно определить число колебаний, через которое амплитуда уменьшится в определенное число раз.

Логарифмический декремент затухания - величина, равная натуральному логарифму от декремента затухания

l = lnD = ln(e^βΤ) = βT. (4.32)

Зная логарифмический декремент затухания l и период колебаний Т, можно записать закон убывания амплитуды в виде

А = А₀×e^-(l/T)×t. (4.33)

Таким образом, логарифмический декремент затухания характеризует затухание колебаний за период. По величине он обратен числу колебаний, совершаемых за то время, за которое амплитуда колебаний уменьшится в "e" раз (l=1/N_e). Если за время t амплитуда уменьшится в "e" раз, то система за это время совершит N_e = t/T колебаний.

Силы трения и сопротивления влияют на частоту колебаний. При достаточно большом трении замедление колебаний может оказаться настолько значительным, что колебания прекратятся, практически едва начавшись. Такие колебательные движения называются апериодическими. В этом случае:

1) при β®ω₀ частота колебаний 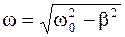®0 - убывает, а период колебаний 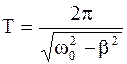®¥, т.е. возрастает;

2) при β>ω₀ характер процесса зависит от начальных условий (x₀ и v₀ = dx₀/dt):

а) 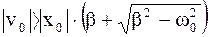- это условие будет выполнено, если выведенной из положения равновесия системе сообщить достаточно сильный толчок к положению равновесия;

б) v₀ = 0 – выполняется, если системе сообщается толчок недостаточной силы.

Для характеристики колебательной системы пользуются понятием добротности Q, которую при малых значениях логарифмического декремента затухания можно определить по формуле

Q = π/λ = π×N_e = π/(βT₀) = ω₀/(2β). (4.34)

Добротность пропорциональна числу колебаний N_e, совершаемых за время t (время релаксации), за которое амплитуда уменьшится в "e" раз.

Для механической колебательной системы с массой m, коэффициентом жесткости k и коэффициентом трения r, добротность определяется соотношением

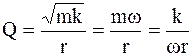. (4.35)

4.4. Вынужденные колебания гармонического осциллятора под действием синусоидальной силы. Дифференциальное уравнение вынужденных колебаний и его решение.
Амплитуда и фаза вынужденных колебаний

Вынужденными колебаниями называются такие, которые совершаются системами под действием внешней (вынуждающей) силы, изменяющейся по какому-либо закону, например гармоническому.

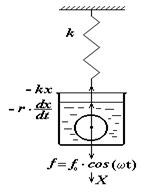Рис.4.6

Рассмотрим колебательную систему – груз, присоединённый к пружине (рис.4.6). Пусть на груз действует гармоническая сила

. (4.36)

Эта сила называется вынуждающей. Частота её изменения – , амплитуда – 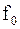. С учетом вынуждающей силы можем записать

или

. (4.37)

Применяя полученные ранее значения b и w₀, получим

. (4.38)

Рассмотрим уравнение (4.38) в простом случае, когда :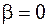

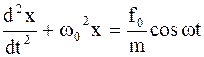. (4.39)

Естественно предположить, что с течением времени тело будет совершать гармонические колебания с частотой вынуждающей силы , т.е.

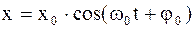. (4.40)

Причём 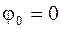, т.к. 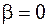. После подстановки (4.40) в (4.39) получим

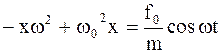. (4.41)

Откуда имеем

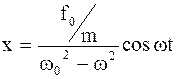. (4.42)

При 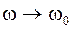амплитуда вынужденных колебаний стремится к бесконечности. Однако в действительности амплитуда возрастает, но остаётся конечной, т.к. существует диссипация энергии. На рис.4.7 показана зависимость амплитуды вынужденных колебаний 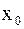от частоты изменения вынуждающей силы .

Решая дифференциальное уравнение (4.38), учитывающее затухание, можно получить следующую зависимость 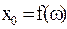и j= (w):

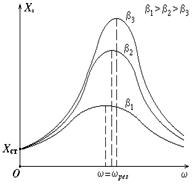Рис.4.7

; (4.43)

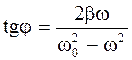. (4.44)

Именно зависимость представлена на рис.4.7 графически.

Исследование функции 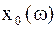на экстремум можно осуществить, исследуя на экстремум подкоренное выражение в формуле (4.43). Для чего приравняем производную к нулю:

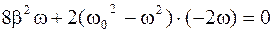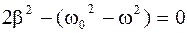. . (4.45)

Частота вынуждающей силы, при которой амплитуда колебаний системы достигает максимума, называется резонансной . Из (4.45) получаем

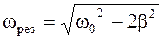. (4.46)

Таким образом, можно записать

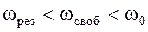. (4.47)

При совпадении частоты изменения вынуждающей силы с частотой резонансных колебаний системы амплитуда колебаний достигнет максимальных значений. Подставляя в формулу (4.43) выражение резонансной частоты, находим максимальное значение амплитуды колебаний

. (4.48)

Амплитуда резонансных колебаний тем больше, чем меньше коэффициент затухания и чем больше амплитуда вынуждающей силы.

Представляют интерес два предельных случая: случай очень низких частот 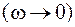и случай очень высоких частот 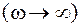изменения вынуждающей силы. Переходя к соответствующему пределу в формуле (4.43), мы получим:

а) на низких частотах 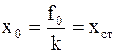, т.е. выполняется закон Гука;

б) на высоких частотах 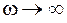, , 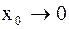т.е. в результате преобладания сил инерции смещение тела из положения равновесия убывает.

Более строгая теория колебаний утверждает, что уравнение вынужденных колебаний (4.38) является дифференциальным, неоднородным, второго порядка, решением которого является выражение вида:

x = x₁ + x₂ = x₀×e^-bt×sin(ω't + φ₀') + x₀×sin(ωt + φ), (4.49)

где ;

x₁ = x₀×e^-bt×sin(ω't + φ₀') – решение однородного уравнения;

x₂ = x₀×sin(ωt + φ).

И только тогда, когда колебания системы будут установившимися (t®¥), решение уравнения (4.38) можно описать только вторым слагаемым

x₂ = x₀×sin(ωt + φ). (4.50)

Из формулы (4.43) вытекает, что при малом затухании (т.е. при β<<ω₀) амплитуда при резонансе приближенно равна

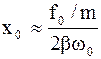. (4.51)

Разделим (4.51) на смещение x от положения равновесия под действием постоянной силы f₀, равное f₀/mw₀². В результате получим

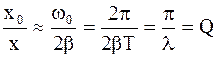. (4.52)

Таким образом, добротность показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы от положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы (это справедливо только при небольшом затухании).

С явлением резонанса приходится считаться при конструировании машин и сооружений. Собственная частота колебаний этих устройств ни в коем случае не должна быть близка к частоте возможных внешних воздействий. Так, например, собственная частота вибраций корпуса корабля или крыльев самолета должна сильно отличаться от частоты колебаний, которые могут быть возбуждены вращением гребного винта или пропеллера. В противном случае могут возникнуть вибрации, которые могут вызвать катастрофу.

Вместе с тем явление резонанса часто оказывается весьма полезным, особенно в акустике, радиотехнике и т.д.

Методы возбуждения вынужденных колебаний различны: путем непосредственного воздействия на колебательную систему (раскачка маятника периодическими толчками) - чаще всего называемые вынужденными; путем периодического изменения параметров колебательной системы (длины подвеса маятника) - так называемое параметрическое возбуждение колебаний; либо благодаря развитию неустойчивостей и возникновению самосогласованных колебательных движений внутри самой системы - так называемые автоколебания.

Особое значение при возбуждении колебаний имеет явление резонанса, заключающееся в резком увеличении амплитуды колебаний при приближении частоты внешнего воздействия к некоторой резонансной частоте, характеризующей систему. Если последняя линейна и параметры ее не зависят от времени, то резонансные частоты совпадают с частотами ее собственных колебаний, и соответствующий отклик тем сильнее, чем выше добротность. Раскачка происходит до тех пор, пока энергия, вносимая извне (например, при каждом отклонении маятника), превышает потери за период осцилляций. Для линейных колебаний энергия, получаемая от источника, пропорциональна первой степени амплитуды, а потери растут пропорционально ее квадрату, поэтому баланс энергий всегда достижим.

При больших амплитудах колебания становятся нелинейными, происходит смещение собственной частоты системы и обогащение их спектра гармониками и субгармониками. Ограничение амплитуды колебаний может быть обусловлено как нелинейной диссипацией энергии, так и уходом системы из резонанса. При возбуждении колебаний в системах с распределенными параметрами максимум амплитуды достигается в случае пространственно-временного резонанса. В этом случае не только частота внешнего воздействия, но и его распределение по координатам, хорошо "подогнаны" к структуре нормальной моды или, на языке бегущих волн, когда наступает совмещение не только их частот (резонанс), но и волновых векторов (синхронизм).

Существует некоторый выделенный класс вынужденных колебаний, в котором внешнее воздействие, не являясь чисто колебательным (например, мгновенный удар), имеет, однако, настолько богатый частотный спектр, что в нем всегда содержатся резонансные частоты системы. Например, заряженная частица, пролетающая между двумя металлическими плоскостями, возбуждает почти весь набор нормальных электромагнитных колебаний и волн, свойственный этой системе. К этому можно отнести черенковское излучение или тормозное излучение частицы в однородных средах, когда и спектр внешних воздействий, и спектр собственных колебаний - оба сплошные, т.е. в них представлены все возможные частоты. Наконец, есть и совсем аномальный случай вынужденных колебаний в системах с непрерывным спектром собственных частот типа ротатора (маховик, колесо, электромагнитное поле и т.п.), где вращательное движение (а следовательно, и два ортогональных колебательных движения) может возбуждаться силами, неизменными во времени.

Параметрическое возбуждение колебаний возникает при периодическом воздействии на те параметры системы, которые определяют величину запасенной колебательной энергии: у маятника - это длина нити или масса груза (но не коэффициент трения); в электрическом контуре - это индуктивность и емкость (но не сопротивление).

При определенных условиях в такой нелинейной колебательной системе могут возникать непрекращающиеся самоподдерживающиеся колебания, или автоколебания, при которых внешнему источнику отводится лишь функция восполнения потерь энергии на диссипацию. Процесс формирования автоколебаний обычно состоит в последовательном самосогласовании движений. Пусть начальное состояние системы неустойчиво либо по отношению к ничтожно малым флуктуациям (мягкий режим возбуждения), либо по отношению к определенным конечным возмущениям (жесткий режим возбуждения). В любом случае спонтанно (случайно) возникшее колебание начнет увеличиваться по амплитуде (процесс усиления колебания), эти усиленные колебания через элемент положительной обратной связи, обеспечивающий самосогласованность фаз, снова "подаются" в место своего возникновения и снова усиливаются и т.д. Получается очень быстрый (чаще всего экспоненциальный) рост колебаний. Ограничение колебаний наступает из-за рассогласованности фаз, а также из-за конечности энергетических ресурсов.

Дата добавления: 2014-01-06