
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Преобразование шкалы частот ФНЧ
|
|
|
|
Переход от фильтров нижних частот к другим типам фильтров

|
| Рис. 17.16 |
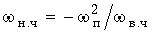 (17.31)
(17.31)
где  n – граничная частота полосы пропускания ФНЧ и ФВЧ.
n – граничная частота полосы пропускания ФНЧ и ФВЧ.
 н.ч = —
н.ч = —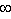 частоте
частоте  в.ч = 0; частоты
в.ч = 0; частоты  н.ч = —
н.ч = — п частоте
п частоте  в.ч =
в.ч =  п; частоты
п; частоты  н.ч = 0 частоте
н.ч = 0 частоте  в.ч =
в.ч = 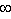 .
.

|
| Рис. 17.17 |
:
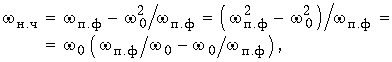 (17.32)
(17.32)
где 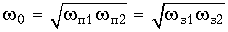 ;
;  п1 и
п1 и  п2 – граничные частоты полосы
п2 – граничные частоты полосы

|
| Рис. 17.18 |
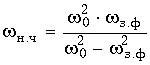 (17.33)
(17.33)
Преобразование схем пассивных LC -фильтров.  ,
,
т. е. в емкостное сопротивление ФВЧ, где C в.ч = 1/ п2 L н.ч.
п2 L н.ч.
Емкостная проводимость:
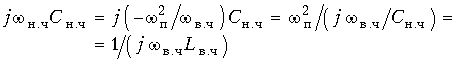
переходит в индуктивную проводимость фильтра ВЧ с индуктивностью L в.ч = 1/  п2 C н.ч.
п2 C н.ч.
Преобразование частоты (17.32) приводит к замене индуктивного сопротивления ФНЧ:
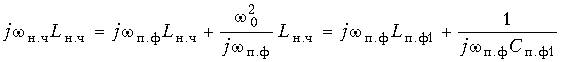
сопротивлением последовательного контура в ПФ с элементами L п.ф1 = L н.ч и C п.ф1 = 1/ ( 02 L н.ч).
02 L н.ч).
Емкостная проводимость ФНЧ:

заменяется в ПФ проводимостью параллельного контура с элементами C п.ф2 = C н.ч и L п.ф2 = 1/ ( 02 C н.ч).
02 C н.ч).
Преобразование передаточных функций активных RC-фильтров.  или
или 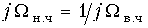 (17.34)
(17.34)
где 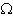 н.ч =
н.ч =  н.ч/
н.ч/ п и
п и 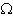 в.ч =
в.ч =  в.ч/
в.ч/  п.
п.
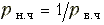 (17.35)
(17.35)
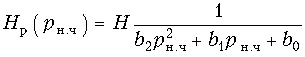 (17.36)
(17.36)
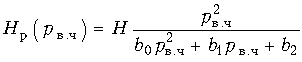 (17.37)
(17.37)
 (17.38)
(17.38)

| |
| Рис. 17.20 | Рис. 17.21 |
Для перехода от НЧ-прототипа к полосовому фильтру воспользуемся (17.33):
 или
или  (17.39)
(17.39)
где 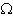 н.ч =
н.ч =  н.ч
н.ч п;
п; 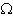 п.ф =
п.ф =  п.ф/
п.ф/ п;
п; 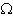 0 =
0 =  0/
0/ п.
п.
Вводя переменную p = j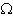 и учитывая, что p 2 = –
и учитывая, что p 2 = –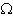 2, находим из (17.39):
2, находим из (17.39):
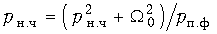 (17.40)
(17.40)
Такая замена переменной p н.ч в (17.36) приводит к передаточной функции полосового фильтра:
 (17.41)
(17.41)
где b '4 = b 2; b '3 = b 1; b '2 = 2 b 2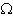 02 + b 0; b '1 = b 1
02 + b 0; b '1 = b 1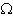 02; b '0 = b 2
02; b '0 = b 2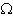 04.
04.
Видим, что при переходе к ПФ порядок передаточной функции удваивается. Передаточную функцию (17.41) можно разбить на произведение передаточных функций второго порядка и каждую из них реализовать отдельной ARC- схемой.
Запишем передаточную функцию ПФ второго порядка:
 (17.42)
(17.42)
Подобную передаточную функцию имеет ARC -схема, изображенная на рис. 17.14, б при Y 1 = G 1, Y 2 = G 2, Y 5 = G 5 и Y 3 = = pC 3, Y 4 = pC 4. Действительно, из (17.28) находим:
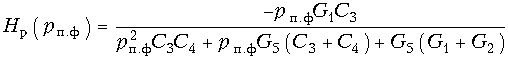 (17.43)
(17.43)
Элементы схемы фильтра (рис. 17.21) определяются сопоставлением (17.42) и (17.43).
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 421; Нарушение авторских прав?; Мы поможем в написании вашей работы!