
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нахождение дискретного сигнала по его z-изображению
|
|
|
|
Для этого можно воспользоваться обратным z -преобразованием (19.29).
Другой способ заключается в том, чтобы разложить функцию X (z) в степенной ряд по степеням z –1. Тогда коэффициенты при степенях z –1 будут, в соответствии с формулой (19.28), отсчетами дискретного сигнала x (k).
Процедура деления здесь не приведена из-за ее громоздкости, хотя выражения полиномов, стоящих в числителе и знаменателе X (z), не слишком сложные.
Более эффективным способом нахождения x (k) по известному X (z) является способ подобный методу разложения на простейшие дроби в преобразованиях Лапласа.
Пример. Найдем общий член xk дискретного сигнала x (k), которому соответствует z -изображение, заданное в предыдущем примере
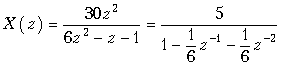 .
.
Функция X (z) имеет полюсы в точках z 1 = 1/2 и z 2 = –1/3, или, что то же, в точках z 1–1 = 2 и z 2–1 = –3.
Разложим X (z) на сумму простых дробей:
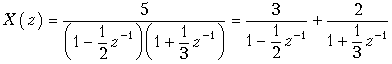 .
.
Коэффициенты в числителях каждой дроби вычисляются так же, как при разложении входного сопротивления z (p) реактивных двухполюсников при синтезе их по схеме Фостера:
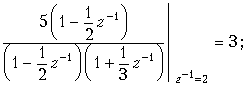
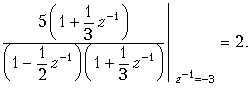
Подобно тому, как формула (19.33) представляет сумму ряда (19.32), простые дроби в (19.16) являются суммами рядов
 и
и 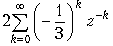 .
.
Поскольку z -преобразование – это линейная операция, то последовательность x (k) состоит из суммы двух последовательностей:
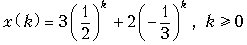 .
.
После выполнения операции возведения в степень k получим отсчеты дискретного сигнала
 и т. д.
и т. д.
Свойства z -преобразования. Так же как и для преобразований Лапласа и Фурье, существуют теоремы для z -преобразования. Приведем наиболее важные теоремы одностороннего z -преобразования.
Теорема линейности (суперпозиции).Сумме дискретных сигналов соответствует сумма их z -изображений. Если дискретным сигналам x (k) и y (k) соответствуют z -изображения X (z) и Y (z), то
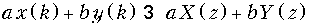 ,
,
где a и b – некоторые числа.
Доказательство теоремы выполните самостоятельно, используя выражение (19.28) для расчета z -изображения дискретного сигнала.
Теорема опережающего сдвига. Если дискретному сигналу x (k) соответствует одностороннее z -преобразование X (z), то сигналу, сдвинутому на один интервал дискретизации, x (k + 1) соответствует z -преобразование z (X (z) – x (0)).
Математическая запись теоремы имеет вид
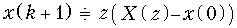 ,
,
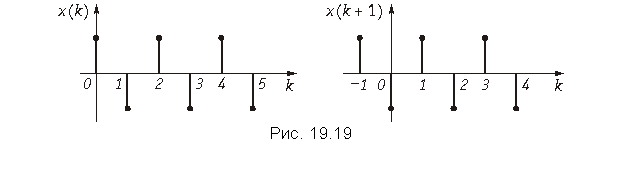
Чтобы доказать теорему, воспользуемся основным выражением (19.28) для расчета z -преобразования дискретных сигналов x (k) и x (k + 1), а также графиками, приведенными на рис. 19.19.
 ;
;
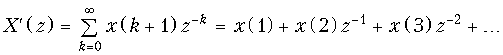 .
.
Сравнивая X (z) и X ¢(z), получаем X ¢(z) = z (X (z) – x (0)), что и требовалось доказать.
Очевидно, что теорема опережающего сдвига выполняет ту же самую роль, что и теорема дифференцирования для преобразований Лапласа.
Теорема задержки. Математическая запись теоремы имеет вид
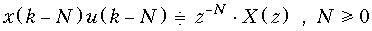 .
.
В теореме задержки u (k) – это дискретные отсчеты функции единичного скачка (рис. 19.20)
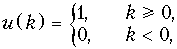

а u (k – N) – это дискретные отсчет функции u (k), задержанной на N интервалов дискретизации (рис. 19.25).
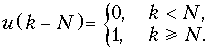
Доказательство вытекает из основного выражения (19.28) для z -преобразования.
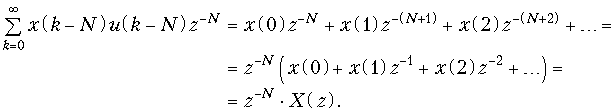
При доказательстве учтено, что единичная ступенчатая функция обращается в нуль при отрицательных значениях ее аргумента, т. е. при n < N. Из теоремы задержки в частности следует, что сдвиг дискретного сигнала на один интервал дискретизации T соответствует умножению z -преобразования на оператор z –1, поэтому часто z –1 называют оператором единичной задержки в z -области.
Теорема умножения на ak. Математическая запись теоремы имеет вид
 .
.
Теорема умножения наn.
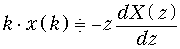 .
.
Теоремы умножения дискретного сигнала x (k) на ak и на k можно также доказать, используя формулу (19.28). Предлагаем проделать это самостоятельно.
Теорема свертки. Свертке дискретных сигналов x (k) и h (k) соответствует произведение их z -преобразований
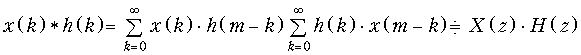 .
.
Эту теорему мы приводим здесь без доказательства. При необходимости с ним можно познакомиться в специальной литературе.
Пример. Найдем z -преобразование функции единичного отсчета, задержанной на N интервалов дискретизации.
Найдем z -преобразование дискретного d -импульса d(k) (рис. 19.4), используя выражение (19.28)
 .
.
Используя теорему задержки, найдем z -изображение сигнала d(k – N)
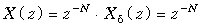 .
.
На рисунке 19.4 приведен также график задержанной функции единичного отсчета для частного случая N = 2.
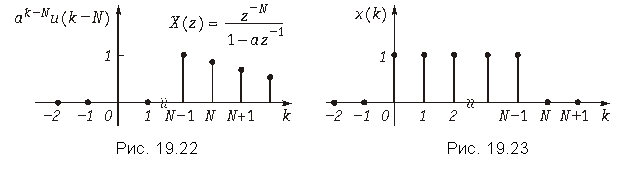
Пример. Найдем z -преобразование функции
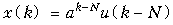 .
.
В одном из примеров мы уже находили, что z -преобразование сигнала ak имеет вид (19.33) X (z) = 1/(1 – az –1).
Используя теорему задержки, получаем
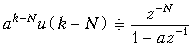 .
.
При a = 1 имеем:
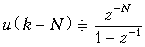 .
.
Графики дискретных сигналов u (k – N) и ak – Nu (k – N) приведены на рис. 19.21 и 19.22.
Пример. Найдем z -преобразование дискретной последовательности x (k) = = kak, k 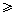 0.
0.
Поскольку z -изображение последовательности ak известно (19.15), то, используя теорему умножения на k, получим
 .
.
Пример. Найдем z- преобразование дискретной последовательности из N отсчетов единичной амплитуды (рис. 19.23)

Сигнал x (k) можно представить как разность двух сигналов
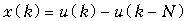 .
.
Из теорем линейности и задержки легко получить z -преобразование
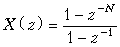 ,
,
что совпадает с формулой для частичной суммы геометрической прогрессии
 .
.
Табл. 19.1 – Краткая таблица односторонних z -преобразований
Дискретный сигнал x (k), k 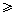 0 0
| z -преобразование 
|

| 
|

| 
|
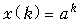
| 
|
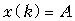
| 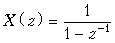
|

| 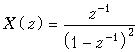
|
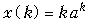
| 
|

| 
|

| 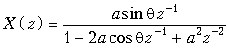
|
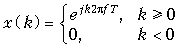
| 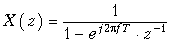
|
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1690; Нарушение авторских прав?; Мы поможем в написании вашей работы!