Z-преобразование и его свойства

При анализе и синтезе дискретных и цифровых цепей широко применяют так называемое z-преобразование. Это преобразование играет такую же основополагающую роль по отношению к дискретным сигналам, как преобразование Лапласа по отношению к аналоговым сигналам.

Z-преобразование дискретного сигнала. Заменим в уравнении (19.8) j w на комплексную переменную p:

(19.24)

таким образом, мы получим изображение по Лапласу дискретного сигнала. Оригинал, т. е. сам дискретный сигнал можно определить с помощью обратного преобразования Лапласа (7.4):

(19.25)

Уравнение (19.25) определяет всю дискретную последовательность . Для определения одного, k -го отсчета формула (19.25) примет вид

(19.26)

Следует однако отметить, что X_T (p) является трансцендентной функцией переменной р вследствие наличия в (19.24) и (19.26) множителя e ^{± pkT}.

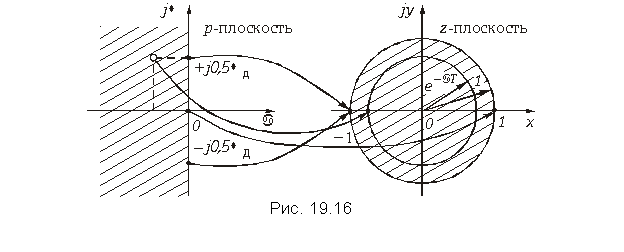
Для перехода к рациональным функциям осуществим замену переменных:

(19.27)

Тогда формула (19.24) примет вид:

(19.28)

Равенство (19.28) называют прямым односторонним z-преоб­разованием.

Обратное z -преобразование определяется формулой:

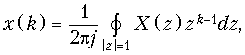(19.29)

где интегрирование осуществляется по окружности с радиусом | z | = 1.

Доказать справедливость (19.29) можно следующим образом. Пусть X (z) – функция комплексной переменной z, аналитическая в области | z | > r ₀. Раскроем ряд (19.28):

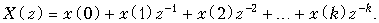(19.30)

Домножим левую и правую часть (19.30) на z^{k –1}:

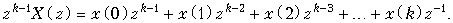(19.31)

Возьмем контурный интеграл от левой и правой части (19.31) вдоль кривой, лежащей целиком в области аналитичности и охватывающей все полюсы X (z) и учтем равенство Коши:

Тогда все слагаемые, кроме k- го обратятся в нуль:

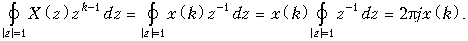
Отсюда непосредственно следует (19.29), что и требовалось доказать.

Дата добавления: 2014-01-06