
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интерполяционные формулы для равноотстоящих узлов
|
|
|
|
Рассмотрим формулу Ньютона (2.7) и предположим, что узлы являются равноотстоящими, а именно, 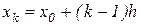 , где
, где 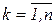 . Сделаем в ней замену
. Сделаем в ней замену 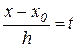 и учтя (2.11), получим
и учтя (2.11), получим
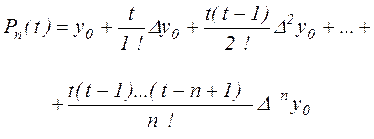 (2.13) (2.13)
|
Это и есть многочлен Ньютона для равноотстоящих узлов, а погрешность интерполяции при его использовании оценивается выражением (2.12).
Отметим, что с увеличением порядка значение конечной разности  убывает. Поэтому нередко требуемая точность вычисления значения функции достигается при меньшем количестве слагаемых, т.е. при меньшем числе использованных узловых точек. В связи с этим, в зависимости от расположения значения x среди массива значений x0 , x1, … xn на основе (2.7) формируют частные формулы, используемые для интерполяции в начале, конце и середине таблицы. Рассмотрим эти случаи.
убывает. Поэтому нередко требуемая точность вычисления значения функции достигается при меньшем количестве слагаемых, т.е. при меньшем числе использованных узловых точек. В связи с этим, в зависимости от расположения значения x среди массива значений x0 , x1, … xn на основе (2.7) формируют частные формулы, используемые для интерполяции в начале, конце и середине таблицы. Рассмотрим эти случаи.
Пусть значение x близко к x0 . Тогда выбирая для интерполяции узловые точки x0 , x0 + h, x0 +m h получим
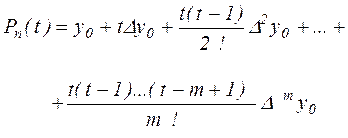 (2.14), (2.14),
|
её погрешность, в соответствии с (2.12)
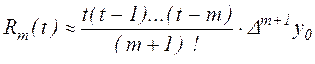
|
Пусть теперь значение x близко к xn, т.е. к концу таблицы. Тогда выбирая для интерполяции узлы xn, xn – h,…, xn –mh и сделав замену 

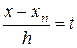 из (2.7) получаем
из (2.7) получаем
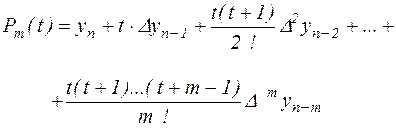 (2.15), (2.15),
|
погрешность интерполяции
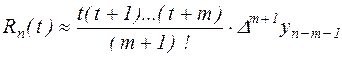 . .
|
Если значение x близко к некоторому xk, расположенному в средней части таблицы, то для интерполяции обычно используют точки xk, xk + h, xk –h, …, xk+mh, xk-mh Соответствующий интерполяционный многочлен также получается из (2.7) и после замены 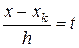 принимаем
принимаем
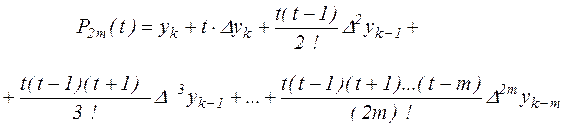 (2.16), (2.16),
|
его погрешность оценивается выражением.
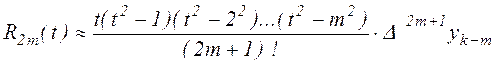 . .
|
Интерполяционному многочлену (2.16) можно придать более симметричный вид. Так, разбивая нечётные слагаемые, начиная с третьего, на два, и группируя с чётными, получим
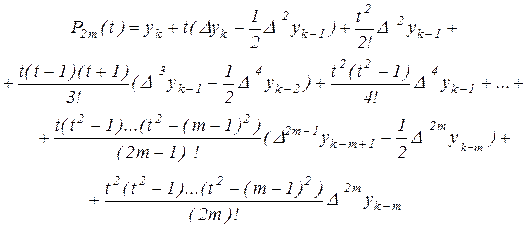
Представим теперь разности в скобках в виде
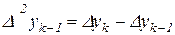 ,
, 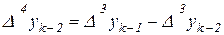 и т.д., получим многочлен,
и т.д., получим многочлен,
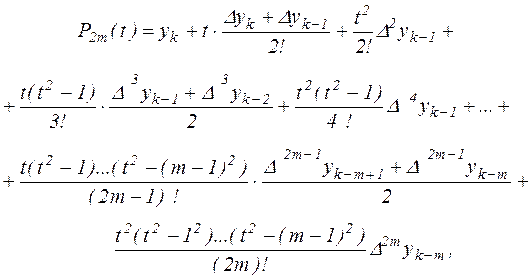
|
который называется интерполяционным многочленом Ньютона – Стирлинга.
2.9. Сплайн – интерполяция
Одним из недостатков рассмотренных методов является высокая степень интерполяционного многочлена, что не всегда является желательным. Разбиение же исходного отрезка на частичные и построение на них отдельных интерполяционных многочленов приводит к тому, что в точках стыка многочленов производные разрывны. Этого недостатка лишены интерполирующие функции, построенные на основе сплайнов.
| Сплайном на отрезке [a, b]называется функция, непрерывная на отрезке вместе со своими производными до заданного порядка включительно, которая на частичных промежутках этого отрезка описывается различными алгебраическими многочленами. |
Рассмотрим методику построения сплайна, основанного на алгебраических многочленах третьей степени, т.е. так называемую, кубическую сплайн – интерполяцию.
Как и ранее, считаем заданной таблицу значений функции 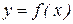 в точках a=x0 , x1, x2 , …, xn = b. На каждом из отрезков [ xi-1, x i ] многочлен Pi(x) будем искать в виде
в точках a=x0 , x1, x2 , …, xn = b. На каждом из отрезков [ xi-1, x i ] многочлен Pi(x) будем искать в виде
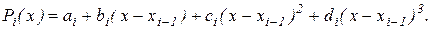
Таким образом, общее число многочленов равно n, а число неизвестных коэффициентов,- 4n. Поэтому для их определения необходимо такое же количество условий.
Потребуем, чтобы каждый многочлен в крайних точках своего отрезка удовлетворял условиям
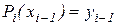 ,
, 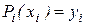 ,
, 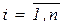 ,
,
что даёт 2n соотношений. Далее, потребуем, чтобы во внутренних узловых точках первая и вторая производные интерполирующей функции были непрерывными, т.е.
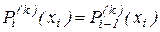 ,
, 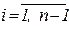 ,
, 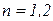 .
.
Это даёт ещё 2(n-1) ограничений. Для получения двух недостающих можно дополнительно потребовать, что в крайних точках отрезка интерполирующая функция имела нулевую кривизну, т.е.,
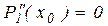 ,
, 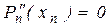
Таким образом, для определения коэффициентов многочленов имеем систему уравнений.
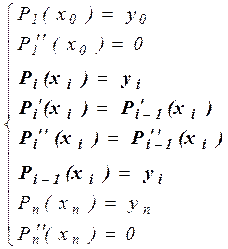
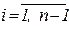 ,
,
которая оказывается линейной. В том случае, когда узловые точки являются равноотстоящими, т.е. 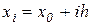 , она существенно упрощается и принимает вид
, она существенно упрощается и принимает вид
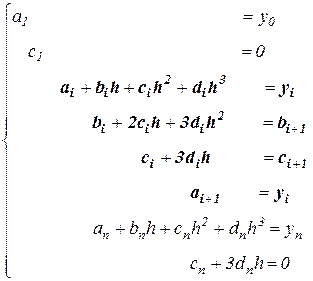
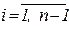 .
.
В частности, для трёх равноотстоящих узлов, т.е. n=2, имеем

которая легко решается в общем виде. Действительно, из 1-го, 2-го, 5-го и 6-го уравнений следует  ,
, 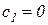 ,
, 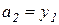 и
и 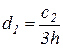 , а оставшаяся часть после традиционных преобразований приводится к треугольному виду
, а оставшаяся часть после традиционных преобразований приводится к треугольному виду
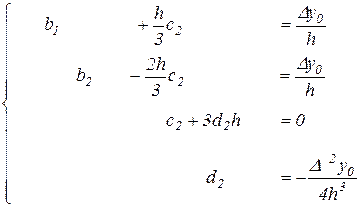 .
.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1794; Нарушение авторских прав?; Мы поможем в написании вашей работы!