Потоки в транспортных сетях

ТРАНСПОРТНЫЕ СЕТИ

Транспортной сетью Т называется совокуп­ность двух объектов:

1. Связного графа 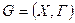, обладающего следующими свой­ствами:

¨ в графе отсутствуют петли,

¨ в графе существует одна и только одна вершина 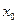такая, что обратное отображение для нее 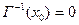, т.е., вершина, которой инцедентны только выходящие дуги,

¨ в графе существует одна и только одна вершина 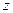, такая, отображение 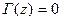, т.е., вершина, которой инцедентны только входящие дуги.

2. Целочисленной неотрицательной функции 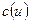, за­данной на множестве дуг графа .

Вершина 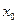называется входом сети, вершина 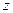— вы­ходом. Значение функции 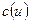на дуге 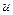называется про­пускной способностью дуги.

(а)

2

x_{0 •}

5

(б)

1

_• z

6

Рисунок 4.6 – Вход (а) и выход (б) транспортной сети

Пусть 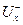— множество дуг, заходя­щих в вершину 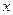, a 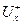— множество дуг, выходящих из вершины 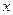. Целочисленная неотрицательная функция 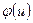, заданная на множестве 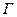дуг графа , называется по­током, если она удовлетворяет следующим условиям:

1. ;

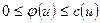2. .

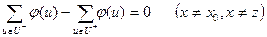Эти свойства можно объяснить таким образом:

1. Поток в дуге не может превышать её пропускную способность.

2. Суммарный поток, входящий в вершину, равен суммарному потоку, выходящему из вершины. Ни в одной вершине графа не должно быть потерь потока.

Сколько потока вытекает из входной вершины 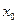, столько его втекает в выходную вершину .

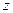Следствие: 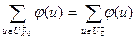= φ _z,

где φ _z – поток транспортной сети.

Рассмотрим подмножество вершин графа 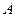, которое является подмножеством всех вершин таких, что , .

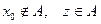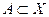U 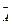- множество дуг, входящих в подмножество ;

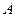U 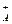- множество дуг, выходящих из подмножества .

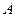Разрезомтранспортной сети называется объединение этих множеств: .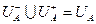

Свойства разреза:

1. Так как разрез включает выход сети, то общий поток через разрез будет равен потоку транспортной сети:

φ _z =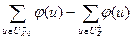. (4.1)

2. Пропускной способностью раз­реза является сумма пропускных способностей дуг, входящих в разрез:

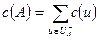. (4.2)

Так как φ (u) ≤ C (u) (4.3), то, заменив в (4.1) φ (u) на C (u), и учитывая (4.2), получим:

φ_z ≤ C (A) (4.4),

т.е., поток транспортной сети не превышает пропускную способность любого разреза.

3

1 2

x₀ 2 1 1 z

6 5

3

A

Рисунок 4.7 – Разрез 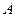транспортной сети

Лемма: Для любого потока 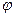и любого разреза 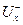справедливо соотношение .

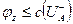Доказательство.

В силу того, что выход сети 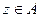, для величины потока 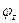справедливы соотношения: .

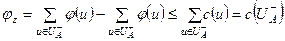Следствие. Если для некоторого потока 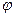и некоторого разреза 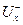выполняется равенство 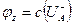, то поток 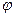обладает наибольшей величиной.

Дата добавления: 2014-01-06