Алгоритм Форда и Фалкерсона нахождения максимального потока транспортной сети

Задача нахождения наибольшего потока в транспортной сети

Постановка задачи:

при заданной конфигурации транспортной сети, когда определены структура графа и пропускные способности дуг, найти наибольшее значение потока,, которое может быть пропущено по данной транспортной сети, и распределение этого потока по дугам транспортной сети.

Дуга 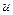называется насыщенной, если поток по этой дуге равен её пропускной способности, т.е. .

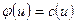Поток 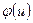называется полным, если каждый путь из 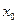в 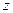, составляющий данный поток, содержит хотя бы одну насыщенную дугу.

Основан на теореме Форда и Фалкерсона:

Максимальный поток в сети равен минимальной пропускной способности разреза.

Алгоритм Форда и Фалкерсона:

1. Перенумеровать произвольным образом вершины транспортной сети , отличные от 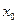и .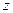

2. Построить произвольный поток на транспорт­ной сети (например, положить).

3. Просмотреть пути, соединяющие вход сети 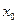с выходом 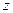. Если поток 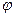полный — перейти к пункту 4. В противном случае рассмотреть путь 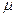, соединяю­щий 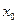с 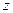, все дуги которого не насыщены. Построить новый поток :

=

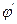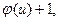
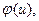
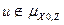
Повторить этот процесс до получения полного потока .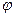

4. Присвоить целочисленные метки вершинам сети и знаки «+» или «—» дугам по правилам:

а) входу 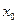присвоить метку 0;

б) если вершина получила некото­рую метку, а 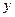— еще непомеченная вершина, то вершине 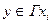, такой что 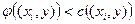присвоить метку 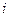, а дуге 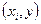- знак «+»; вершине 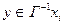, такой что , присво­ить метку 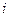, а дуге 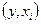- «-». Остальные непомечен­ные вершины и дуги метки и знака не получают;

в) повторить процесс, описанный в пункте 4б) до тех пор, пока не прекратится появление новых отмечен­ных вершин и дуг. Если в результате процесса 4б) вер­шина 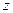не получит метки, то поток обладает наиболь­шей величиной. В противном случае перейти к пункту 5.

6. Рассмотреть последовательность отмеченных вер­шин , каждая из которых имеет метку, равную номеру последующей вершины, и после­довательность дуг 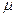(не обязательно путь), соединяю­щих последовательные вершины из 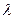. Построить новый поток :

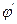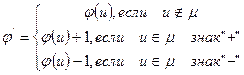
Перейти к пункту 4.

Примечание 1. Если в найденном пути номера индексов совпадают, то вторую вершину можно опустить, перейдя непосредственно к меньшему индексу, что не приведёт к изменению потока. Таким образом, - максимальный поток. Дальнейшее увеличение возможно только при увеличении пропускной способности дуг.

Примечание 2. При программной реализации алгоритма первый этап можно опустить, а начинать со второго этапа, индексируя вершины графа при потоке .

Дата добавления: 2014-01-06