Пример решения транспортной задачи по критерию стоимости

Имеется однородный груз в трёх пунктах отправления. Требуется доставить груз в четыре пункта назначения при соблюдении условия баланса. Стоимость перевозки 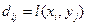. Т.е. сколько груза вести из каждого пункта отправления в 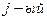пункт назначения, чтобы стоимость перевозки была минимальной.

Таблица 4.11 – Таблица стоимости и количества перевозимого груза

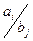
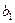
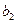
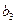
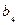
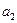
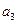
1.Проверяем условие баланса: .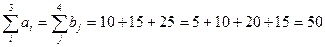

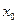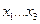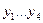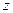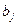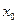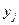2.Строим транспортную сеть. Выбираем начальную вершину и соединяем её с вершинами дугами с пропускной способностью равной а_i. Вершины соединяют с выходом сети с пропускной способностью равной . Считаем, что стоимость перевозки из в и из в 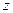равна нулю.

3. Находим кратчайший путь из 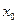в 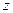. Присваиваем всем вершинам 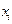метку 0. Начиная с вершины 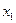присваиваем всем вершинам 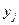метку, которая равна стоимости перевозки груза по соединяющей их дуге. Рядом с меткой ставим вершину, из которой была присвоена метка. Проводя следующую индексацию из 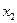, заменяем метки вершин 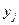, если стоимость дуги меньше, чем метка, которую имеет вершина. Метку делаем постоянной. Заканчиваем индексацию, когда пройдены все вершины 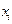. Из меток вершин 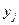выбираем минимальную и присваиваем метку выходу сети 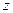. По вершинам возле постоянных меток возвращаемся назад и отмечаем кратчайший путь.

4. Применяем алгоритм метода частичных потоков.

x₁ 8 y₁

10 3 5

2 5 y₂ 10

x₀ 15 x₂ z

7 y₃ 20

25 1 9 15

x_{3 4} y₄

Рисунок 4.12 – Транспортная сеть для таблицы 4.11

1-ый этап. Кратчайший путь: .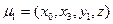

Стоимость по дуге: .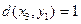

Частичный поток: 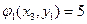. Стоимость груза: .

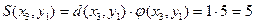Осталось груза: .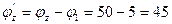

x₁ y₁

10 5

y₂ 10

x₀ 15 x₂ z

y₃ 20

25 15

x₃ y₄

Рисунок 4.13 – Первый путь перевозки груза по ТС

x₁ y₁

y₂ 10

x₀ 15 x₂ z

y₃ 20

20 5 15

x₃ y₄

Рисунок 4.14 – Второй путь перевозки груза по ТС

x₁ y₁

y₂

x₀ 5 x_{2 10 ыы}z

y₃ 20

20 5 15

x₃ y₄

Рисунок 4.15 – Третий путь перевозки груза по ТС

x₁ y₁

y₂

x₀ 5 x₂ 10 z

y₃ 20

20 5 5

x₃ y₄

Рисунок 4.16 – Четвёртый путь перевозки груза по ТС

x₁ y₁

y₂

x₀ 5 x₂ 10 z

y₃ 20

15 5

x₃ y₄

Рисунок 4.17 – Пятый путь перевозки груза по ТС

x₁ y₁

y₂

x₀ 5 x₂ 10 z

y₃ 5

5 15

x₃ y₄

Рисунок 4.18 – Шестой путь перевозки груза по ТС

Таблица 4.12 – Решение транспортной задачи в виде таблицы

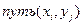
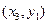
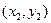
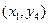
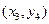
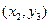
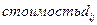
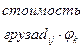
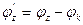
Стоимость перевозки всего груза:

.

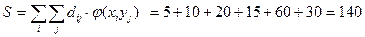Транспортная задача по критерию времени

Дана транспортная сеть с некоторым распределением потока φ_z (см. транспортную сеть, полученную в результате решения транспортной задачи по критерию стоимости).

Задача:

Найти такое распределение потока, которое бы обеспечивало минимальное время его распределения T_min.

Здесь веса дуг трактуются как время, необходимое для доставки груза по данной дуге: d_ij = t_ij.

Решение заключается в следующем:

1) Находится некоторое распределение потока φ_z по дугам транспортной сети. Т.е. получаем некоторый частичный граф G₁ ’, в который включаются дуги, участвующие в передаче потока. Каждая из этих дуг входит в состав пути из x₀ в z и определяет время прохождения данного потока t_μ. Таких путей x₀ в z может быть конечное множество:

G₁ ’ = { μ ₁, μ ₂, …, μ_n }, которым соответствует время прохождения по пути

Т = { t_μ1, t_μ2, …, t_μn }.

Общее время прохождения потока:

Т = max t_μ. μ Î G₁ ^’

Для нашего случая, когда Т = max {1, 1, 2, 3, 6, 4} = 6.

Т.о. Т_min = min T = min max t_μ – минимакс.

2) Находим частичное решение. Выведем из графа G₁ ’ наиболее продолжительный путь и введем ранее неиспользованные дуги, у которых вес меньше, чем у выведенной дуги. Во вновь образованном графе G₂ ’ перераспределим исходный поток φ_z, используя алгоритм нахождения максимального потока в графе (Форда и Фалкерсона). Этот пункт повторяем до тех пор, пока выведенные пути наибольшей продолжительности будут возмещаться новым распределением потока φ_z.

Для обеспечения сквозной нумерации при индексации вершин перенумеруем вершины y_j таким образом:

y_j: = x_{n + j}.

Для нашего примера: y_j: = x_{3 + j}.

x₁ y₁ = x₄

10 3 5

2 5 x₅ 10

x₀ 15 x₂ z

x₆ 20

25 1 ₄ 15

x_{3 3} x₇

Рисунок 4.19 – Преобразованная транспортная сеть

После исключения дуги (х₂, х₆) со временем прохождения по ней

t = 6 результирующий поток транспортной сети уменьшается на 5 единиц:

φ_z^’ = φ_z – 5 = 50 – 5 = 45.

К полученному графу добавляем дуги, которые не участвовали в исходном распределении потока, но с длиной меньше 6:

(х₂, х₄), (х₁, х₅), (х₁, х₆) – Т = {3, 5, 4}.

Перераспределим 5 единиц потока, используя данные дуги, пропустив его по пути m = (х₀, х₂, х₄, х₃, х₆, z), применив алгоритм Форда и Фалкерсона нахождения максимального потока в транспортной сети.

Получаем φ_z^’’ = φ_z^’ + 5 = 45 + 5 = 50 = φ_z.

При этом Т₂ = max ­ { t₁₄, t₂₁, t₂₂, t₃₃, t₃₄ } = {2, 4, 1, 4, 3} = 4.

Таким образом граф G₂ будет иметь следующий вид:

x₁ y₁ = x₄

10 5

2 (5) (10) x₅ 10

x₀ 15 x₂ z

(10) x₆ 20

25 _{4 (20)} 15

x_{3 3 (5)} x₇

Рисунок4.20 – Граф G₂ после перераспределения 5 единиц потока

Примечание: Если суммарный поток по дуге (х_i y_j) и (y_j х_i) равен 0, то данная дуга отбрасывается. В нашем примере это дуга (х₃ х₄).

Таблица 4.13 – Решение транспортной задачи по критерию стоимости

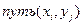
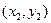
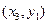
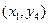
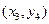
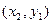
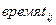
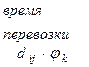
t μ

Таким образом, алгоритм решения данной задачи следующий:

1. Найти начальное распределение потока в транспортной сети, решив, например, транспортную задачу по критерию стоимости. Найти время прохождения потока в данном распределении t_m.

2. Построить новый граф, исключив из начального дугу, обеспечивающую максимальное время прохождения потока, и добавив ранее неиспользуемые дуги, у которых t_ij < t_m.. При этом поток, проходящий по новому пути, будет меньше на величину потока, проходившего по вычеркнутой дуге.

3. Решить задачу нахождения максимального потока в транспортной сети по алгоритму Форда и Фалкерсона. Если удастся пропустить весь заданный поток, то перейти к пункту 2. Иначе алгоритм останавливается. Минимальное время прохождения потока будет определяться последним временем прохождения исходного потока.

Дата добавления: 2014-01-06